Предмет: Геометрия,
автор: marinenko2018
Визначте вид і знайдіть сторони чотирикутника, вершинами якого є середини сторін ромба з діагоналями 8 см і 14 см.
Ответы
Автор ответа:
9
Ответ:
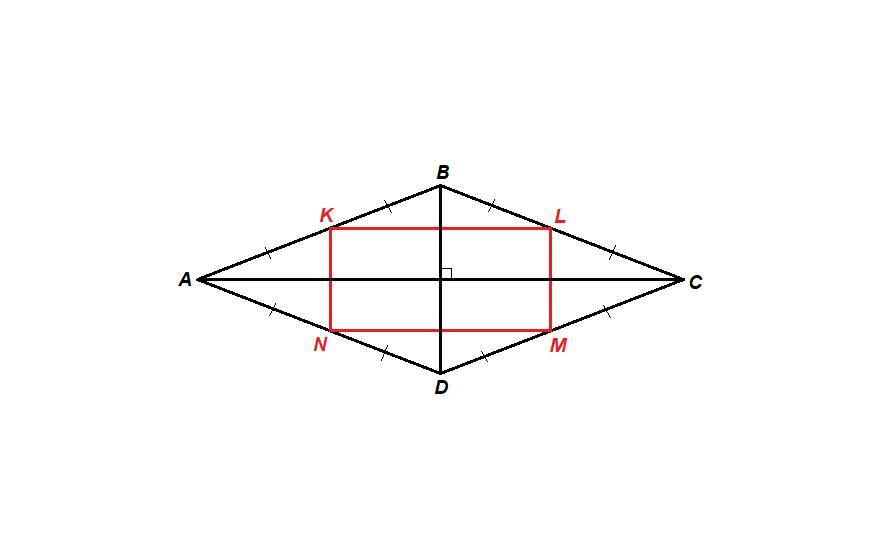
KLMN - прямоугольник.
KL = MN = 7 см
LM = KN = 4 см
Объяснение:
AC = 14 см
BD = 8 см
K, L, M и N - середины сторон AB, BC, CD и AD ромба соответственно.
Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
KL║AC, KL = 1/2 AC = 1/2 · 14 = 7 см как средняя линия ΔАВС.
MN║AC, MN = 1/2 AC = 1/2 · 14 = 7 см как средняя линия ΔADC.
Значит, KL║MN и KL = MN, тогда KLMN - параллелограмм.
KN║BD, KN = 1/2 · BD = 1/2 · 8 = 4 см как средняя линия ΔABD.
LM = KN = 4 см как противоположные стороны параллелограмма KLMN.
АС⊥BD по свойству диагоналей ромба.
Так как KL║AC и KN║BD, то KL ⊥ KN, значит KLMN - прямоугольник.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: сан78дре5
Предмет: Английский язык,
автор: alabamanv
Предмет: Русский язык,
автор: ternowskaya
Предмет: Обществознание,
автор: KrisKreed01
Предмет: Математика,
автор: lolehn0048