Question

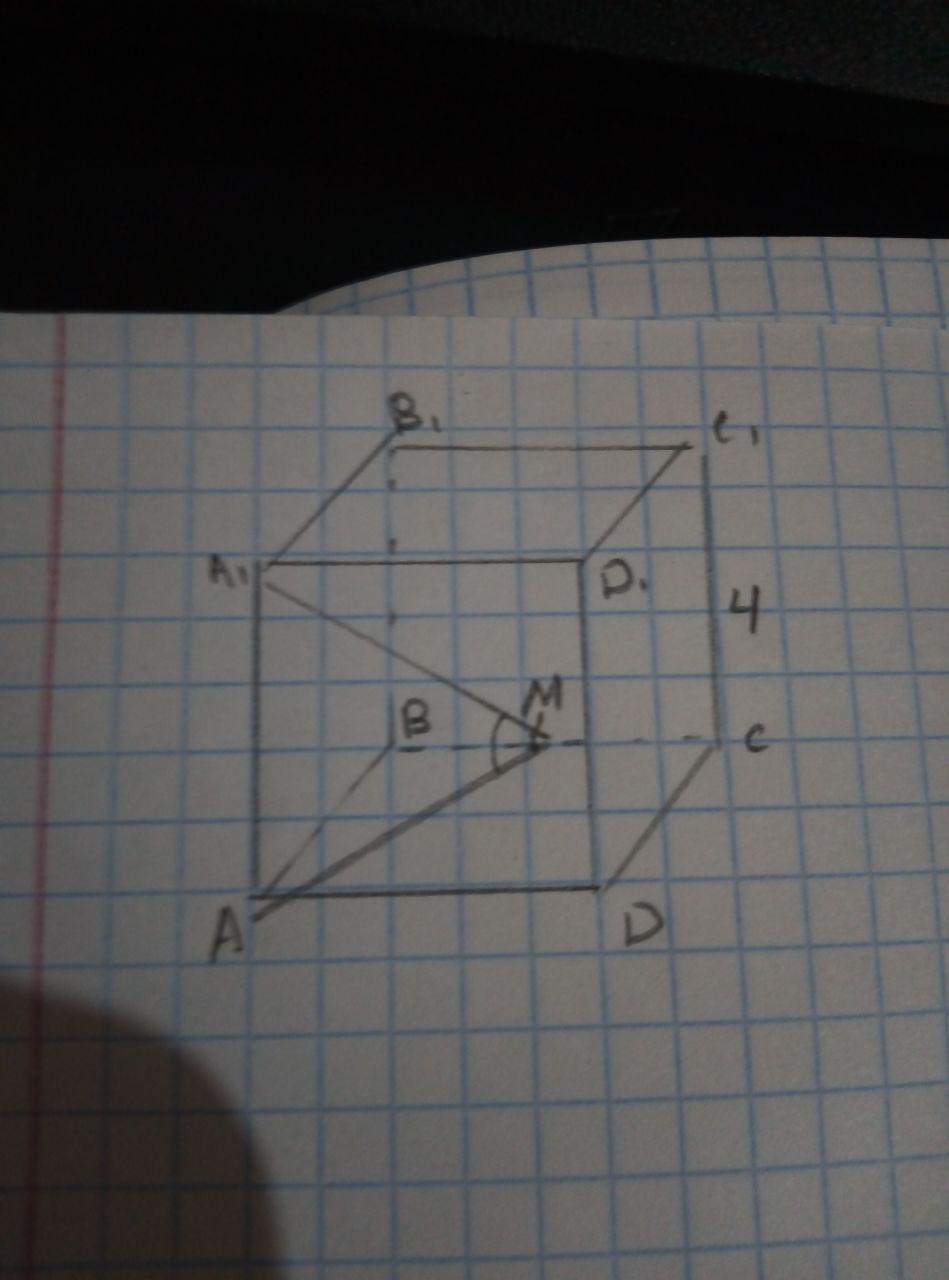
Дана правильная треугольная призма ABCA1B1C1, точка M — середина ребра BC. Найдите косинус угла AMA1, если боковое ребро CC1 равно 4, а сторона основания равна 2$\sqrt{3}$. С рисунком, пожалуйста)

Answer 1

Ответ:

АА1 _L ABC по свойству правильной призмы. Тогда <АА1М=90° и ∆АА1М - прямоугольный. В ∆АВС АМ - медиана, раз он равносторонний - то и высота, откуда ВМ=0.5*ВС=√3, <АMВ=90°. ∆АВМ прямоугольный, AB²=BM²+AM³, откуда АМ=3. ∆А1АМ прямоугольный, A1M²=MA²+AA1², A1M²=3²+4², A1M=5.

cos(<A1MA)=AM/A1M=3/5

Объяснение: