Question

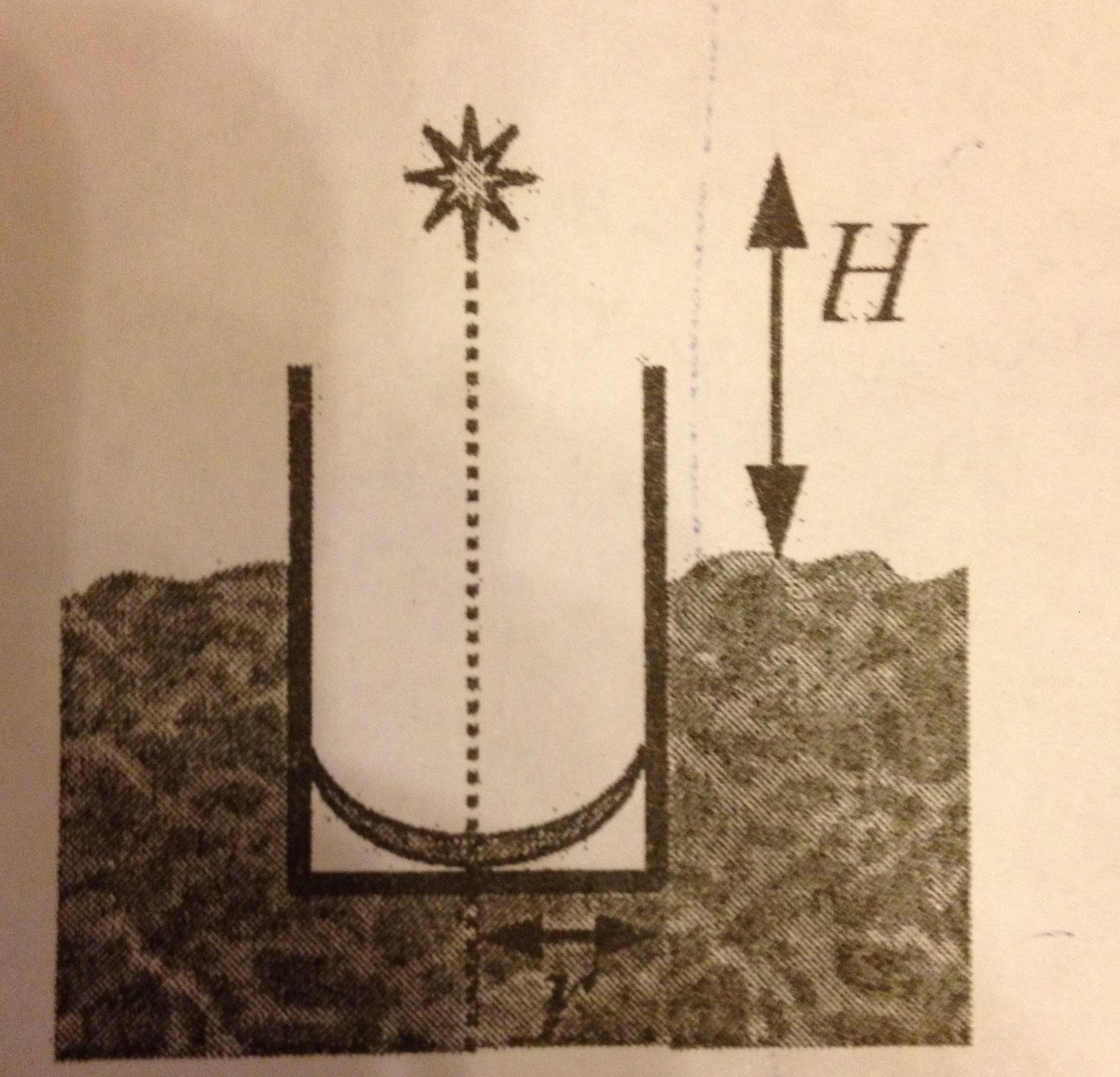
На дне высокого цилиндрического стакана лежит вогнутое зеркало с радиусом кривизны R;
оптическая ось зеркала совпадает с осью стакана. Стакан плавает в жидкости(см. рис.). На высоте H над поверхностью жидкости строго над серединой стакана расположена лампочка. При какой плотности жидкости изображение лампочки окажется на уровне поверхности жидкости? Масса стакана вместе с зеркалом равна M. Радиус дна r.

Answer 1

F=R/2 - фокусное расстояние зеркала
1/F=2/R=1/A+1/B=1/A+1/(A+H)
А - расстояние от зеркала до изображения
В - расстояние от зеркала до источника (до лампочки)
2/R=1/A+1/(A+H)
2*A*(A+H)=R*(2A+H)
A^2+A*(H-R)-RH/2=0
D=(H-R)^2+4*RH/2=H^2+R^2
A=(корень(H^2+R^2)-(Н-R))/2 - расстояние от дна стакана до изображения (до поверхности воды)
M=ro*A*pi*r^2
ro = M/(A*pi*r^2) = M/(((корень(H^2+R^2)-(Н-R))/2)*pi*r^2) = 2*M/((корень(H^2+R^2)-(Н-R))*pi*r^2)  - это ответ