Question

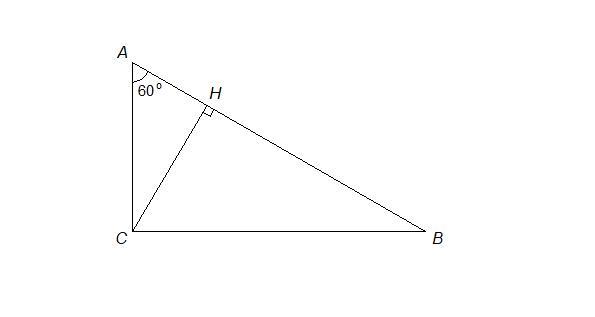
ПОЖАЛУЙСТА ПОМОГИТЕ СРОЧНО ДАЮ 20 БАЛЛОВ!!!!! Острый угол прямоугольного треугольника равен 60 градусам, а гипотенуза равна 72 градусам. Найдите отрезки на которые делит гипотенузу высота, проведенная из вершины прямого угла!!!!!!!

Answer 1

Ответ:

18 см   и   54 см

Объяснение:

AB = 72 см

∠A = 60°

Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

Из ΔАВС:

$\cos \angle A=\dfrac{AC}{AB}$

$AC=AB\cdot \cos \angle A=72\cdot \cos 60^\circ=72\cdot \dfrac{1}{2}=36$  см

Из ΔАСН:

$\cos \angle A=\dfrac{AH}{AC}$

$\boldsymbol{AH}=AC\cdot \cos 60^\circ=36\cdot \dfrac{1}{2}\boldsymbol{=18}$   см

НВ = АВ - АН = 72 - 18 = 54 см