Предмет: Алгебра,
автор: 6665464447458
Помогите!!!! Комплексные числа
Приложения:
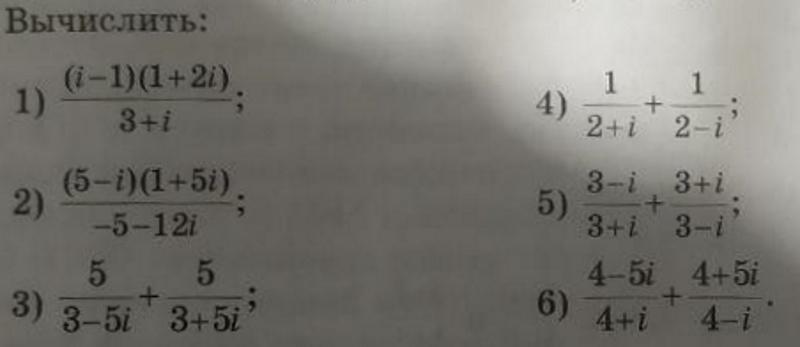
Ответы
Автор ответа:
1
1)
2)
3)
4)
5)
6)
Похожие вопросы
Предмет: Русский язык,
автор: Rita210
Предмет: Английский язык,
автор: todd66
Предмет: Қазақ тiлi,
автор: Kam2504
Предмет: Математика,
автор: девочка237
Предмет: Химия,
автор: vladimirmorozo2