Предмет: Геометрия,
автор: Vyakuschenko
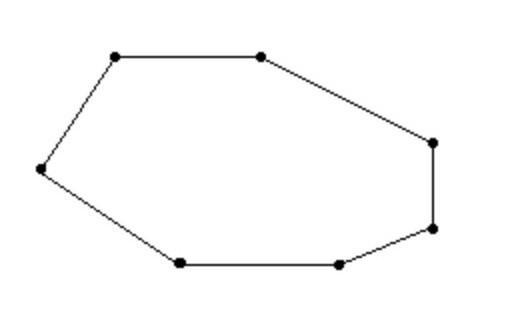
Определи, сколько диагоналей можно провести в данном многоугольнике.
Ответ:
диагонал(-ей, -и).
Название данного многоугольника:
десятиугольник
семиугольник
шестиугольник
пятиугольник
девятиугольник
восьмиугольник
четырёхугольник
треугольник
Приложения:
Ответы
Автор ответа:
24
Ответ:
Это семиугольник. У семиугольника 14 диагоналей.
Объяснение:
Семиугольник: 7 сторон, 7 вершин
"Формула для вычисления числа диагоналей многоугольника: d = n(n-3)/2, где d – число диагоналей, n – число сторон многоугольника.
Используя распределительное свойство, эту формулу можно записать так: d = (n^2 - 3n)/2."
d = (n^2 - 3n)/2 = (7^2 - 3*7)/2 = (49 - 21)/2 = 28/2 = 14 диагоналей
SAM0407:
неправильно
а как же правильно тогда?
там немного другой ответ
Похожие вопросы
Предмет: Английский язык,
автор: Greys44
Предмет: Английский язык,
автор: chueva83
Предмет: Русский язык,
автор: khiznichenko
Предмет: Химия,
автор: afgannagiev
Предмет: Математика,
автор: rbbozh