Предмет: Алгебра,
автор: Аноним
памаги те пж алгебра
Приложения:
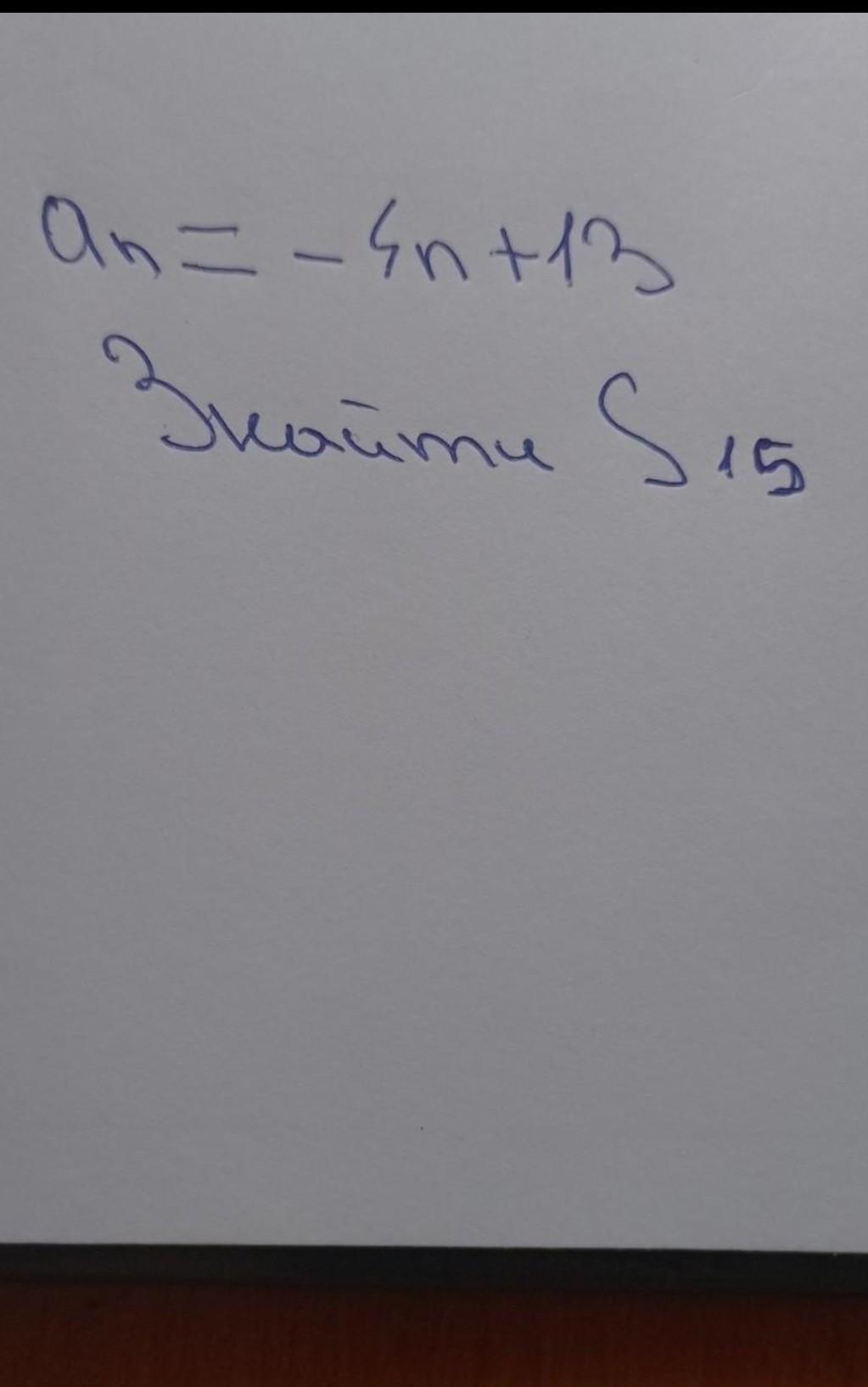
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Числовой ряд задан выражением aₙ = -4n + 13.
Покажем, что это арифметическая прогрессия.
n-й член арифметической прогрессии задается выражением:
aₙ = a₁ + d(n - 1)
Преобразуем заданное выражение:
aₙ = -4n + 13 = 13 - 4n = 9 + 4 - 4n = 9 - 4(n - 1)
aₙ = -4n + 13 = 9 - 4(n - 1) ⇒ это арифметическая прогрессия, в которой первый член a₁ = 9, а разность прогрессии d = -4.
Найдем пятнадцатый член прогрессии:
n = 15, a₁₅ = -4 * 15 + 13 = -60 + 13 = -47
Найдем сумму пятнадцати членов арифметической прогрессии:
Похожие вопросы
Предмет: Русский язык,
автор: tan1283
Предмет: Українська мова,
автор: ВладаАлмазова
Предмет: Қазақ тiлi,
автор: Jenia2014
Предмет: Алгебра,
автор: ImLiza
Предмет: Математика,
автор: Илюминат1337