Предмет: Геометрия,
автор: lavaopen9999
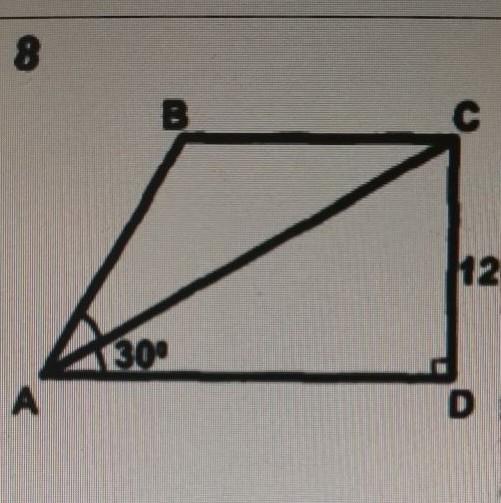
Найти площадь трапеции
Приложения:
Ответы
Автор ответа:
2
Ответ:
В прямоугольном треугольнике катет лежащий против угла 30 равен половине гипотенузы => AC - гипотенуза = 12 * 2 = 24.
AC - биссектриса ∠BAC = ∠CAD = 30°
∠ACD = 180° - (30° + 90°) = 60°
Т.к AC диагональ => ∠BCA = 1/2 * 60°= 30°
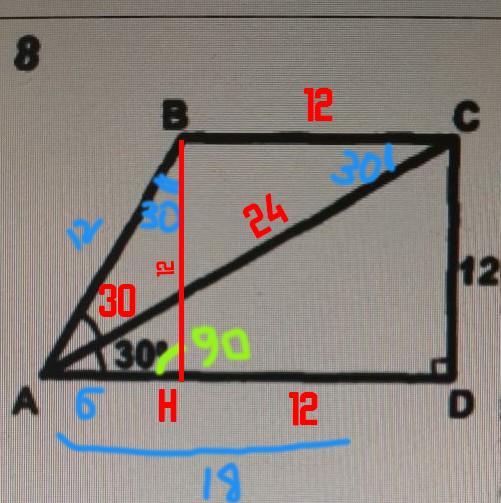
Проведем высоту BH => BC = HD = 12
ΔABC равнобедренный => BC = AB = 12
∠ABH = 180 - (90 + 60) = 30
В прямоугольном треугольнике катет лежащий против угла 30 равен половине гипотенузы => AH = 12 / 2 = 6.
AD = AH + HD = 6 + 12 = 18
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям. => BH = CD = 12
Площадь трапеции равна произведению полусуммы ее оснований на высоту
S = (a+b)/2 * h
S = (12 + 18) / 2 * 12= 180
Приложения:
lavaopen9999:
а можешь ещё с одним помочь?) А я тебе потом больше баллов дам
там тоже надо найти площадь трапеции
Похожие вопросы
Предмет: Українська мова,
автор: ksunlantux
Предмет: Русский язык,
автор: katyabakhorina
Предмет: Русский язык,
автор: 89061191907
Предмет: Физика,
автор: konstandoglo00
Предмет: Алгебра,
автор: neizvestno2016