Предмет: Алгебра,
автор: dmitrijefimov053
Пожалуйста решите интеграл
Приложения:
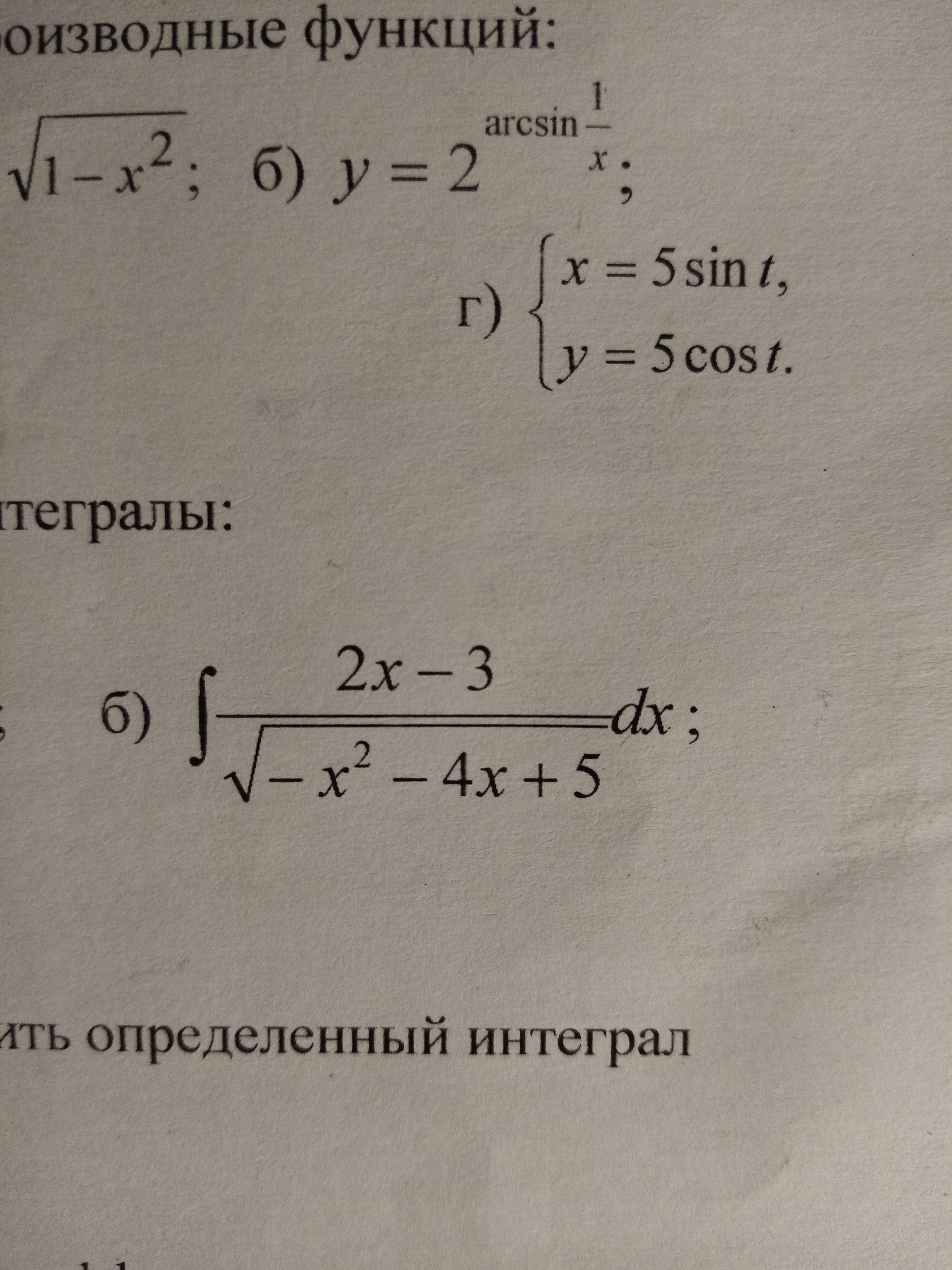
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: hakermax96
Предмет: Русский язык,
автор: birlik595
Предмет: Другие предметы,
автор: maks130
Предмет: Математика,
автор: erikleranatal
Предмет: Математика,
автор: гэлочка