Question

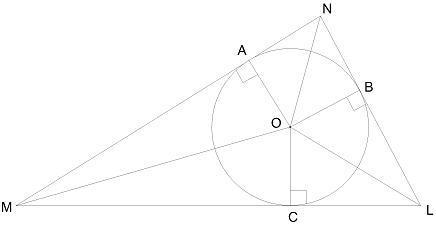
Помощь по Геометрии В треугольник вписана окружность. Вычисли неизвестные углы, если ∢ OMN = 26° и ∢ ONL = 28°. ∢ COA = °; ∢ BOA = °; ∢ COB = °.

Answer 1

Ответ:

< COA = 128°, < BOA = 124°, < COB = 108°

Объяснение:

Центр окружности, вписанной в треугольник, находится на пересечении биссектрис углов треугольника. Поэтому OM, ON и OL - биссектрисы.

Биссектриса делит угол пополам - значит, < OML = < OMN = 26°,

< ONM = < ONL = 28°.

Сумма углов треугольника 180°.

В треугольниках ΔCOM, ΔMOA углы < OCM = 90°, < OAM = 90°.

Тогда < COM = 180° - < OML - < OCM = 180° - 26° - 90° = 64°

< AOM = 180° - < OMN - < OAM = 180° - 26° - 90° = 64°

( * )              < COA = < COM + < AOM = 64° + 64° = 128°

В треугольниках ΔAOM, ΔMOB углы < OBN = 90°, < OAN = 90°.

Тогда < AON = 180° - < ONM - < OAN = 180° - 28° - 90° = 62°

< AOM = 180° - < OMN - < OAM = 180° - 28° - 90° = 62°

( * )              < BOA = < BON + < AON = 62° + 62° = 124°

< COA + < BOA + < СOB = 360° (эти углы составляют полный угол)

< COB = 360° - < COA - < BOA = 360° - 128° - 124° = 108°