Предмет: Математика,
автор: darap3918
решите уравнение методом введения новой переменной
Приложения:
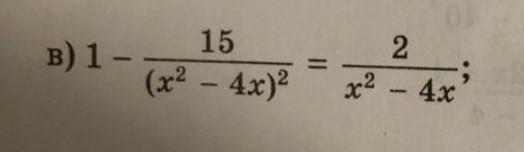
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
ОДЗ:
Замена:
Продолжим решение:
Обратная замена:
Итого:
Уравнение решено!
Похожие вопросы
Предмет: Другие предметы,
автор: bikushka2003
Предмет: Қазақ тiлi,
автор: ketikets
Предмет: Английский язык,
автор: токнт
Предмет: Литература,
автор: ИЛЮХИН10000
Предмет: Математика,
автор: anarrzaev80