Question

Постройте график квадратичной функции y=x2-4x+8​

Answer 1

Ответ:

Решение в разделе "Пошаговое объяснение".

Пошаговое объяснение:

1. Функция $y=x^2-4x+8$ вида $ax^2+bx+c=0$.

2. Функция является квадратичной (график - парабола).

3. Ветви параболы направлены вверх, так как $a=1>0$.

4. Координаты вершины параболы $(2; \: 4)$, так как:

$x_0=-\dfrac{b}{2a}=-\dfrac{-4}{2*1}=-\dfrac{-4}{2}=\dfrac{4}{2}=2 \\ \\ y_0=2^2-4*2+8=4-8+8=-4+8=4$

5. Ось симметрии параболы $x=2$, так как:

$x=-\dfrac{b}{2a}=-\dfrac{-4}{2*1}=-\dfrac{-4}{2}=\dfrac{4}{2}=2$

6. Координаты точек пересечения с осью $Ox$:

$x^2-4x+8=0 \\ \\ D=b^2-4ac=(-4)^2-4*1*8=8-32=-24$

Так как дискриминант меньше нуля, то уравнение не имеет решений

⇒ парабола не имеет точек пересечения с осью $Ox$.

7. Координаты точек пересечения с осью $Oy$:

$(0; \:c)=(0; \: 8)$

То есть координаты точек пересечения с осью $Oy-(0; \: 8)$.

Симметричная ей точка относительно оси параболы:

$\Big(-\dfrac{b}{a}; \: c\Big)=(4; \: 8)$

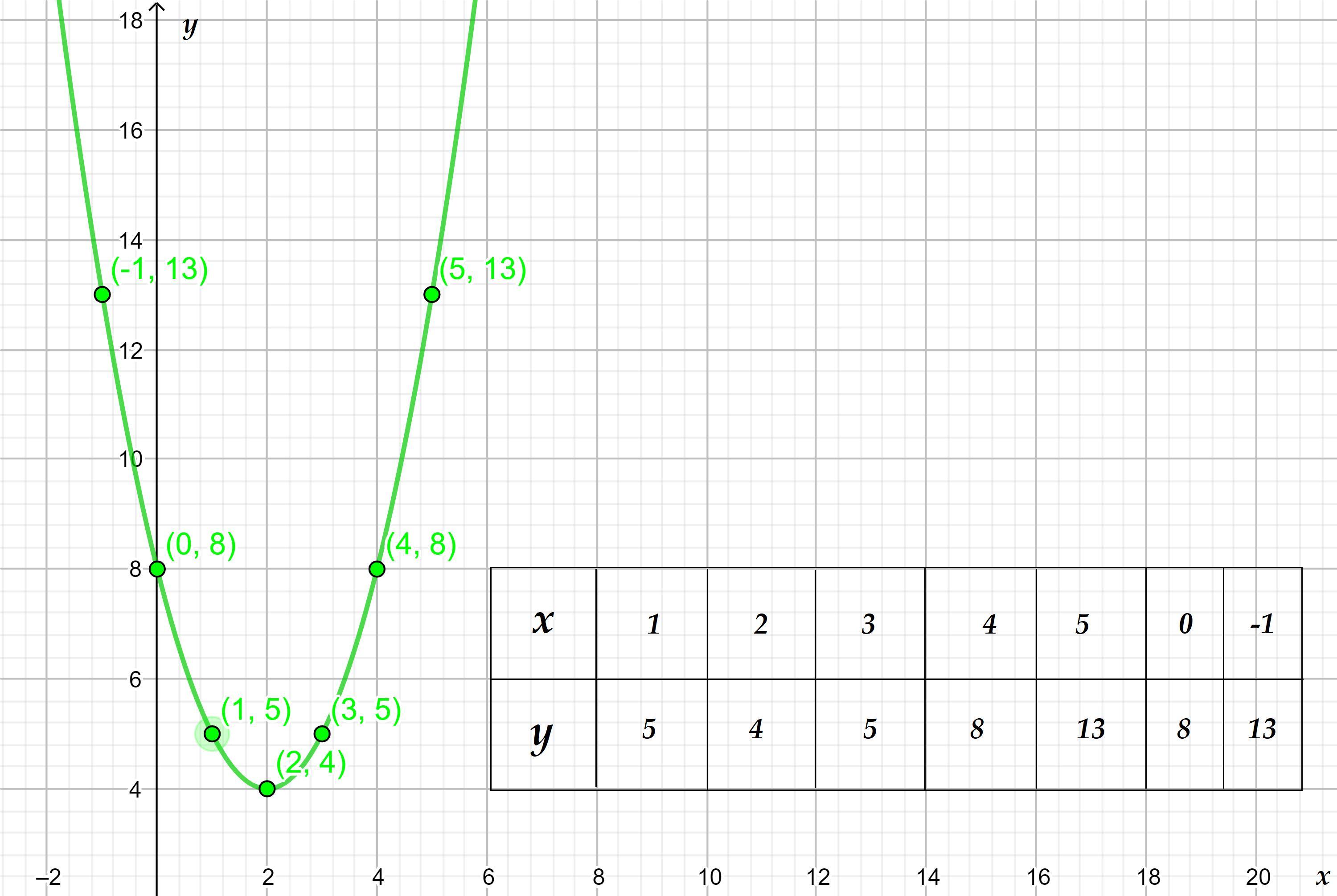
8. Построим таблицу со значениями по оси $Ox$ и по оси $Oy$.