Question

В правильной шестиугольной призме ABCDEFA1B1F1E1F1 все ребра равны 1. Найдите длину вектора а)AC1 б)AD1​

Answer 1

Ответ:

AC₁=2

AD₁=√5

Объяснение:

1. Рассмотрим ΔАВС (см. рис. 1). Он равнобедренный с АВ=ВС=1 и ∠В=120° (как внутренний угол правильного шестиугольника). Опустим  высоту ВО на АС. Получили два равных прямоугольных ΔАВО = ΔСВО с углами 60°,  30° и 90° (т.к. ВО в равнобедренном тр-ке есть биссектрисой).

По теореме Пифагора,

$AO=AB*sin\angle ABO=1*\frac{\sqrt{3} }2} =\frac{\sqrt{3}}{2}$

тогда АС=АО*2=$\sqrt{3}$

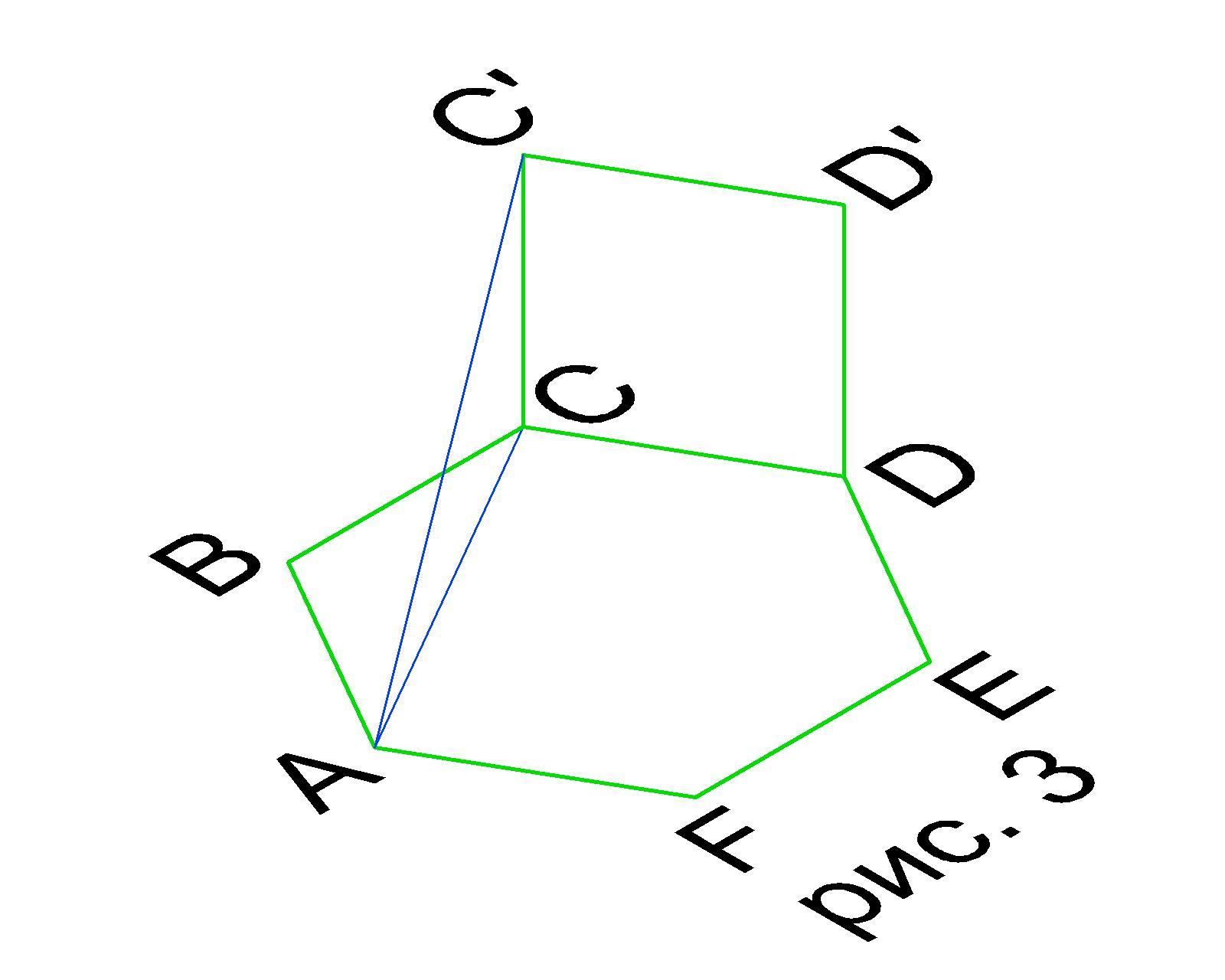
Рассмотрим ΔACC₁ (см. рис. 3). Он прямоугольный с двумя известными катетами

АС=√3, CC₁=1. Гипотенуза АС₁ является искомой величиной.

По теореме Пифагора: $AC_1=\sqrt{AC^{2} +CC_1^{2} } =\sqrt{3+1} =2$

2. Рассмотрим ΔACD. Он прямоугольный с двумя известными катетами

АС=√3, CD=1 (см. рис. 2). Найдем гипотенузу АD.

$AD=\sqrt{AC^{2} +CD^{2} } =\sqrt{3+1} =2$

Рассмотрим ΔADD₁ (см. рис. 4). Он прямоугольный с двумя известными катетами

АD=2, DD₁=1. Гипотенуза АD₁ является искомой величиной.

По теореме Пифагора: $AD_1=\sqrt{AD^{2} +DDC_1^{2} } =\sqrt{4+1} =\sqrt{5}$