Question

20.
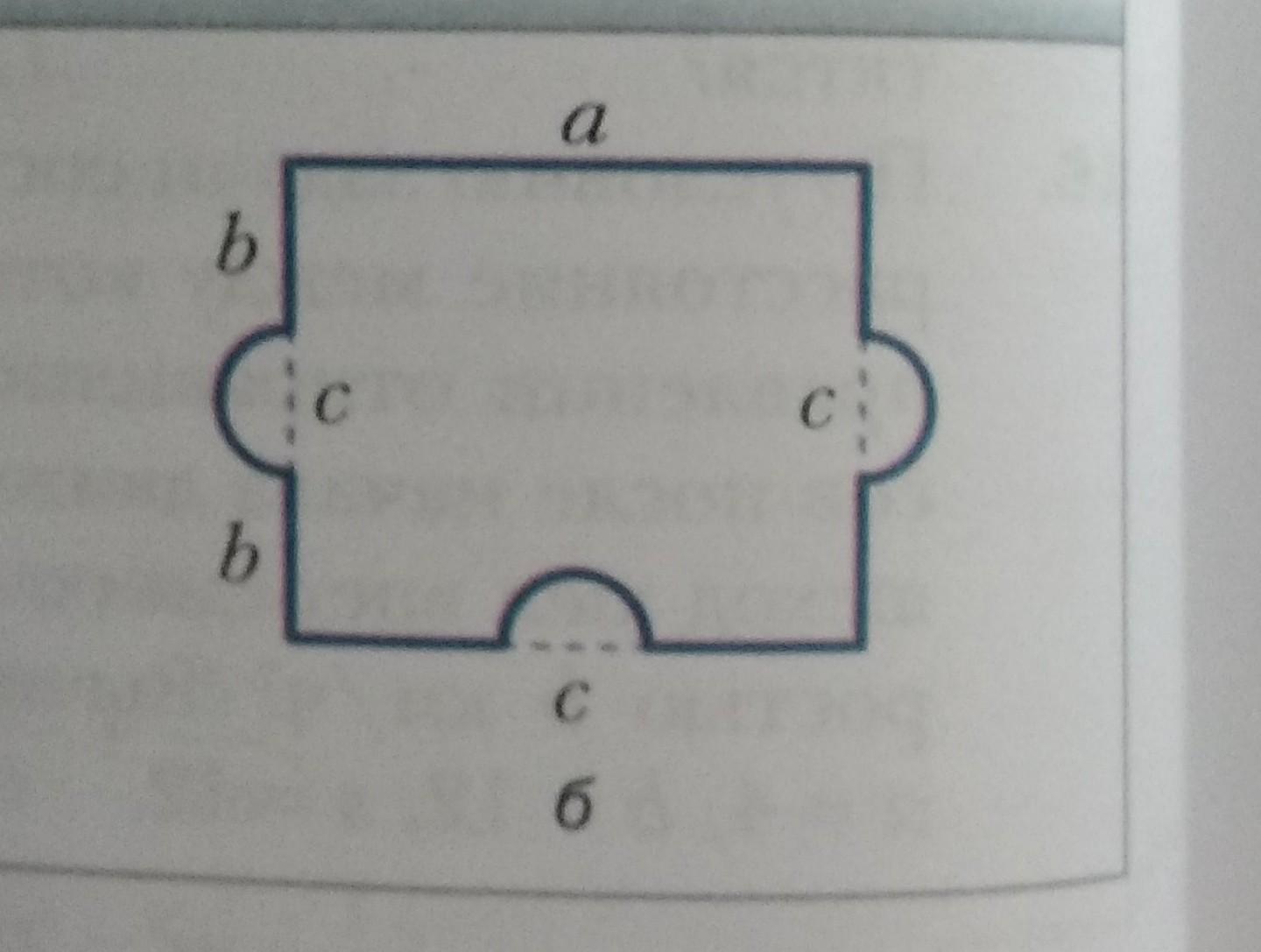
Составьте выражения для вычисления длины синей линии и площади
фигуры, которую она ограничивает (рис. 2).

​

Answer 1

На чертеже полуокружности имеют диаметр, равный  D=с ,  R=c/2 ,  

длина этой полуокружности равна   $l=\dfrac{1}{2}\cdot 2\pi R=\pi R=\pi \cdot \dfrac{c}{2}=\dfrac{\pi c}{2}$

площадь полуокружности равна   $S=\dfrac{1}{2}\cdot \pi R^2=\dfrac{1}{2}\cdot \pi \cdot \dfrac{c^2}{4}=\dfrac{\pi c^2}{8}\ .$

Периметр (длина линии, ограничивающей фигуру) равен

$P=a+(a-c+\dfrac{\pi c}{2})+(2b+\dfrac{\pi c}{2})+(2b+\dfrac{\pi c}{2})=2a+2b-c+\dfrac{3\pi c}{2}=\\\\=2(a+b)+c\, (\dfrac{3\pi }{2}-1)$

Площадь фигуры равна

$S=a\cdot (2b+c)-\dfrac{\pi c^2}{8}+\dfrac{\pi c^2}{8}+\dfrac{\pi c^2}{8}=a\cdot (2b+c)+\dfrac{\pi c^2}{8}$