Предмет: Геометрия,
автор: Spirit425
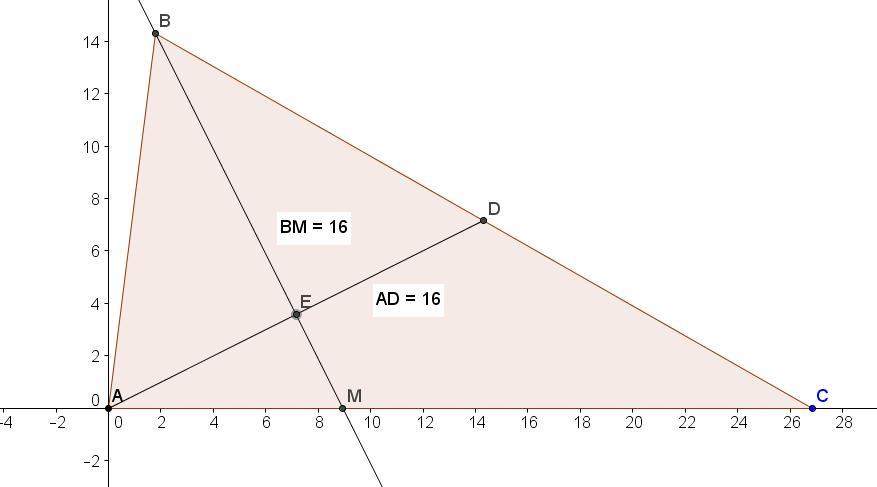
Отрезки AD и BM -- соответственно медиана и биссектриса треугольника ABC, AD перпендикулярно BM, AD=BM=16 см. Найдите стороны треугольника ABC
Приложения:

Ответы
Автор ответа:
0
Обозначим точку пересечения АД и ВМ как Е.
ВЕ перпендикулярно АД, углы равны, значит, АВ = ВД.
Примем АВ = х, тогда ВС = 2х.
Обозначим АМ = у, по свойству биссектрисы СМ = 2у.
Далее используем формулы.
Медиана: 4АД² = 2х² +2(3у)² - (2х)².
4*256 = -2х² + 18у² или, сократив на 2: 512 = -х² + 9у².
Биссектриса: ВМ = (√(х*2х*(3х + 3у)*(3х - 3у))/(х + 2х).
Возведём обе части в квадрат.
9х²*256 = 2х²(9х² - 9у²), сократим на 2, 9 и х²:
128 = х² - у².
Вместо х² подставим его значение из медианы.
128 = -512 + 9у² - у².
8у² = 640 или у² = 80. Отсюда у = √80.
Тогда х² = 128 + х² = 128 + 80 = 208. Отсюда х = √208.
Ответ: АВ = √208, ВС = 2√208, АС = 3√80.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: superlinkina
Предмет: Русский язык,
автор: agapkin2004
Предмет: Алгебра,
автор: misteralmazof
Предмет: Математика,
автор: akselroddasha