Предмет: Алгебра,
автор: Elizabeta14
Решить системы с помощью теоремы виета
Приложения:
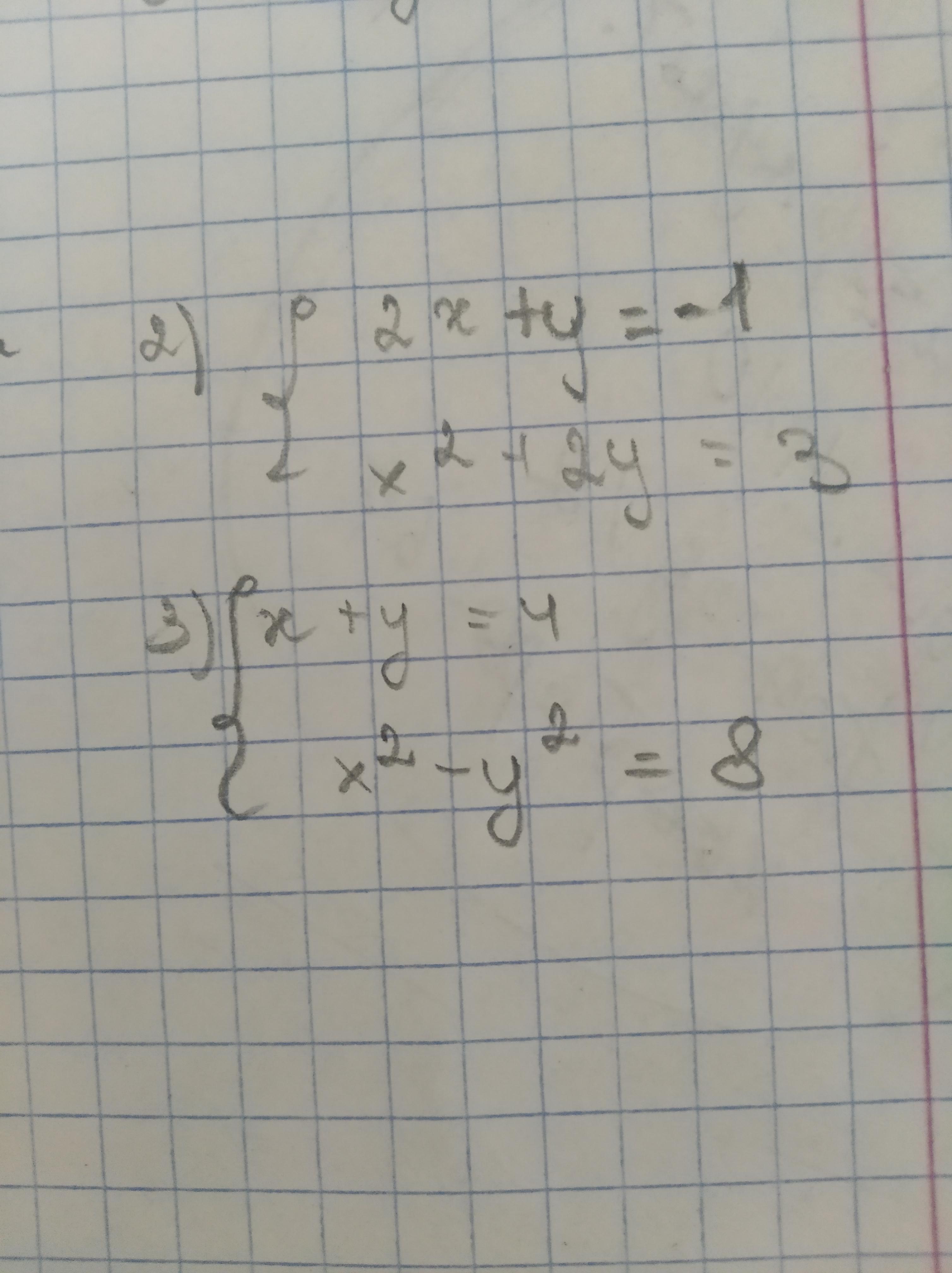
Ответы
Автор ответа:
0
Объяснение:
Суммируем эти уравнения:
Суммируем эти уравнения:
Похожие вопросы
Предмет: Английский язык,
автор: 195618122
Предмет: Русский язык,
автор: 2014Ритуся2014
Предмет: Українська мова,
автор: liza13koval
Предмет: Физика,
автор: Molnarkaa
Предмет: Математика,
автор: danil708