Предмет: Алгебра,
автор: dejbci
1. 6x2 + 18x = 0
2. x2 - 8x + 7 = 0
3. 4x2 - 9=0
4. 3x2 + 5x +6=0
Приложения:
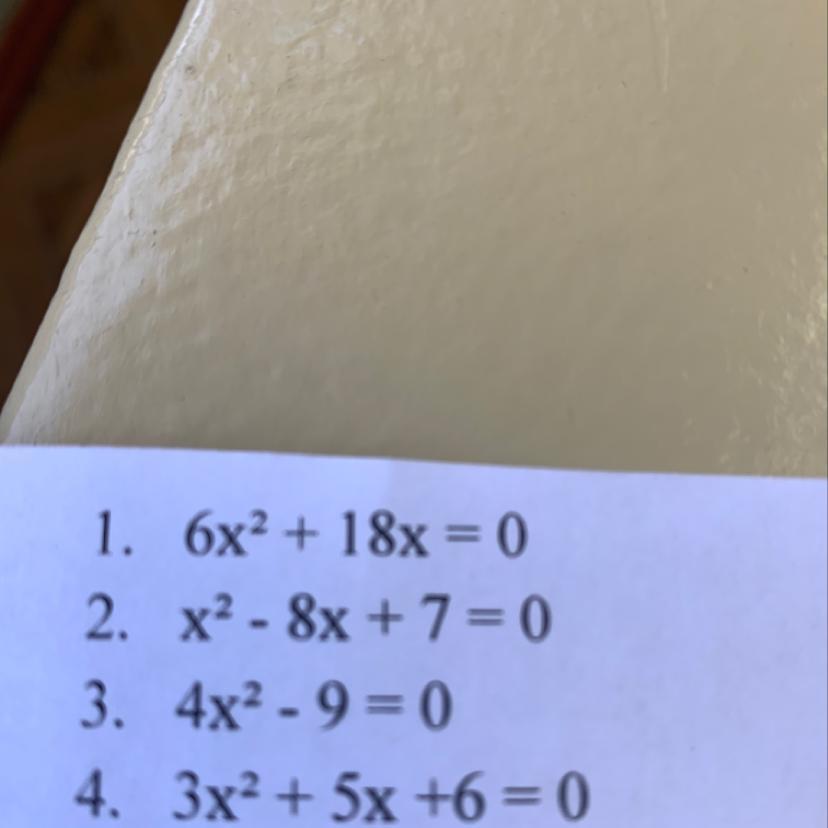
Ответы
Автор ответа:
0
Формула дискриминанта:
Формулы корней:
Решение:
Похожие вопросы
Предмет: Русский язык,
автор: revan2004
Предмет: Русский язык,
автор: MissYana25
Предмет: Английский язык,
автор: katy200371
Предмет: Математика,
автор: zaharhi336