Question

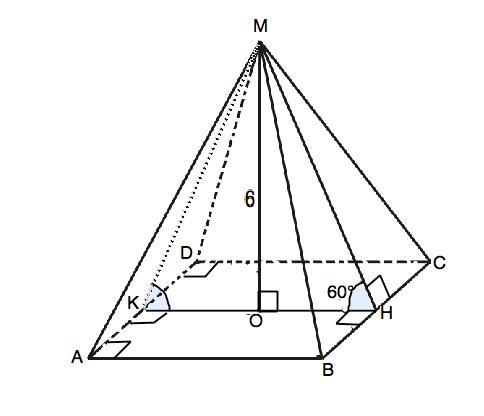
В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60 градусов.Высота пирамиды равна 6 см.Найдите площадь поверхности пирамиды.

Answer 1

Ответ: 144 см²

Объяснение:  

 Основание правильной четырехугольной пирамиды - квадрат,  боковые грани - равнобедренные треугольники, а вершина проецируется в центр основания.

 Обозначим пирамиду МАВСD. МО - высота, МН - апофема. Апофемой называют высоту боковой грани правильной (!) пирамиды; здесь  МН - высота равнобедренного треугольника ВМС.

  МН⊥ВС, ⇒ по т.о 3-х перпендикулярах её проекция ОН⊥ВС. Т.к. О - центр основания, НО=ОК, а КН, сторона ∆ КМН, параллельна и равна АВ.

  ∆ МОН  прямоугольный, МН=МО:sin60°=6:(√3/2)=4√3 см

Так как углы при основании ∆ КМН равны 60°, треугольник КМН равносторонний, КН=МН, АВ=КН=4√3.

Площадь поверхности пирамиды Ѕ(полн)=Ѕ(бок)+Ѕ(осн)

Ѕ(бок)=0,5(МН•ВС)•4=0,5•(4√3•4√3)•4=96 см²

Ѕ(осн)=АВ²=(4√3)²=48 см²

Ѕ(полн)=96+48=144 см²