Предмет: Алгебра,
автор: TrishaElric
70 баллов.
Найдите тангенс угла между прямыми:
а) y = -3/4×x - 1 и y = 3/4 ×x + 2
б) 2y + 3x - 1 = 0 и 3y + 2x - 5 = 0
в) x = 1 и y = -2x + 1
г) x = -3 и 3x + 2y - 3 = 0
Желательно скинуть промежуточные действия, а не только ответ.
Приложения:
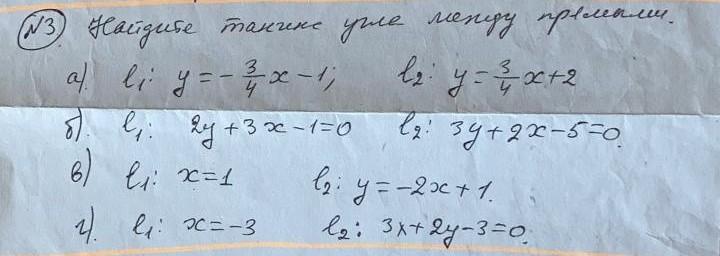
Ответы
Автор ответа:
2
Угол φ между двумя прямыми, заданными уравнениями c угловыми коэффициентами
y=k₁x+b₁ y=k₂x+b₂, вычисляется по формуле: tgφ=(k₂-k₁)/(1+k₁*k₂)
а) y=-3х/4-1 и y=3х/4 +2
tgφ=(3/4+3/4)/(1-9/16)=3*16/(2*7)=24/7=3 3/7
б) 2y+3x-1=0 и 3y+2x-5=0; у=-3х/2 -1/2и у=2х/3 +5/3;
tgφ=(2/3+3/2)/(1-(3*2)*(2/3)); tgφ=∞; φ=90°
в) x = 1 и y = -2x + 1;
cosφ=(1*2+0*1)/(√1*√5)=2/√5; sinφ=√(1-4/5)=1/√5; tgφ=(1/√5):(2/√5)=1/2
г) x = -3 и 3x + 2y - 3 = 0
cosφ=(1*3+0*2)/(√1*√(3²+2²))=3/√13; sinφ=√(1-9/13)=2/√13;
tgφ=(2/√13):(3/√13)=2/3
mhjbjaira77777:
пожалуйста помогиииии мнееее
привет
Ответ к б: 5/12
Автор ответа:
1
Так как для прямой х=const (x=1) угол между прямой и осью ОХ равен 90° , а tg90° не существует, то указать угловой коэффициент прямой невозможно ( ) .
Ответ к в: 1/2
и у меня 1/2 ...
Похожие вопросы
Предмет: Русский язык,
автор: MAXPAUNE
Предмет: Русский язык,
автор: ismajlova2000
Предмет: Другие предметы,
автор: lena23351
Предмет: Алгебра,
автор: ekaterinaabog00