Question

Доведіть, що ѕіn 45° = cos 45°.

Answer 1

Самое простое доказательство:

$sin(45^\circ) = \frac{\sqrt{2} }{2}$ (табличное значение)

$cos(45^\circ) = \frac{\sqrt{2} }{2}$ (табличное значение)

$\frac{\sqrt{2} }{2} = \frac{\sqrt{2} }{2} \Rightarrow sin(45^\circ) = cos(45^\circ)$

Нормально геометрическое доказательство:

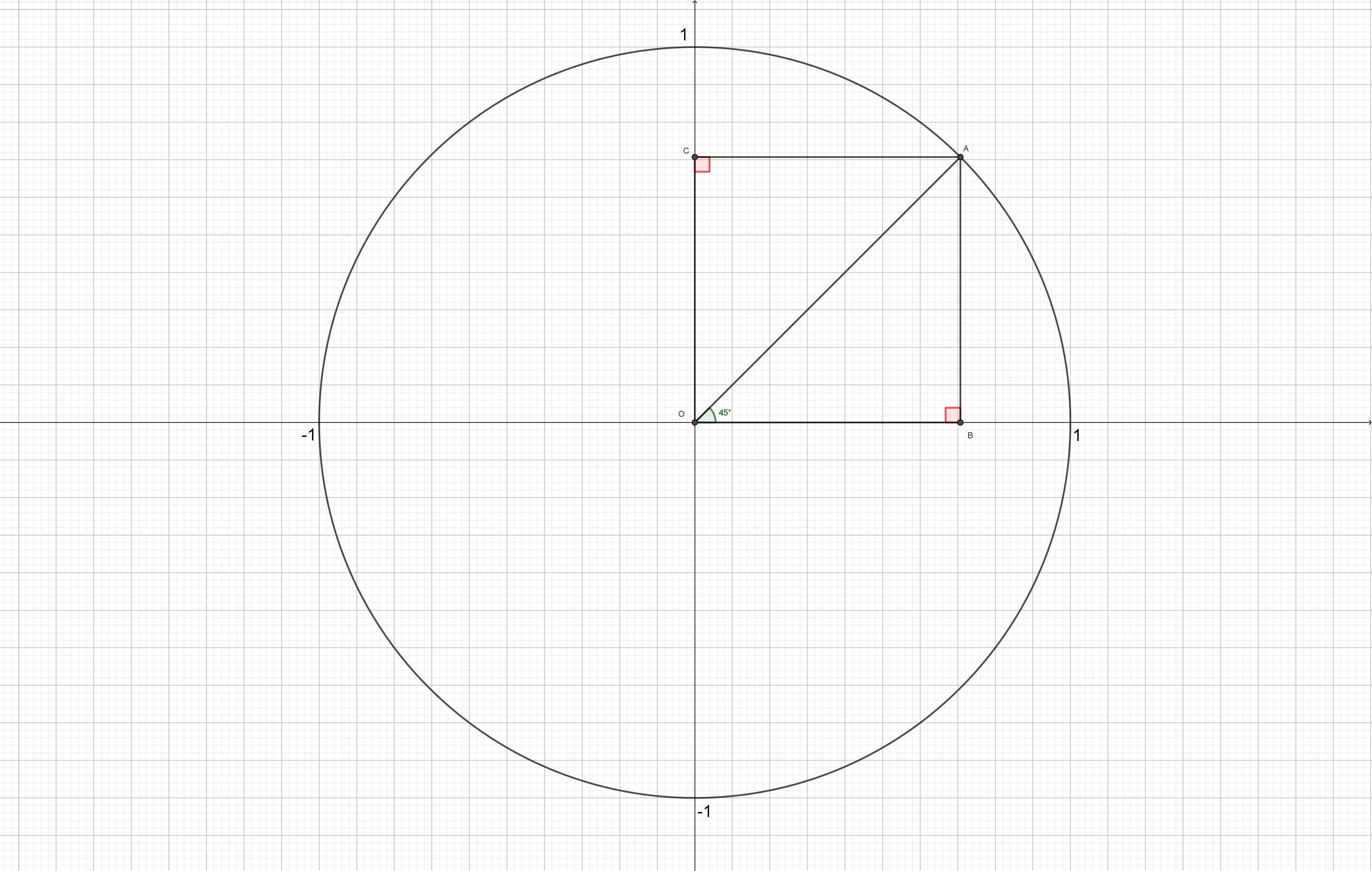
См. Рисунок.

Согласно определению $sin(45^\circ) = OC$, a $cos(45^\circ) = OB$

В ΔOAB ∠OAB = 180° - 90° = 45°, значит ΔOAB - равнобедренный с основанием OA.

В ΔOAC ∠OAC = 180° - 90° = 45°, значит ΔOAC - равнобедренный с основанием OA.

ΔOAB =  ΔOAC по стороне и двум углам. (OA - общая).

Следовательно OC = OB

Значит $sin(45^\circ) = cos(45^\circ)$

============  

Не забывайте нажать "Спасибо", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Успехов в учебе