Предмет: Алгебра,
автор: Maryranta1995
Помогите пожалуйста решить)
Приложения:
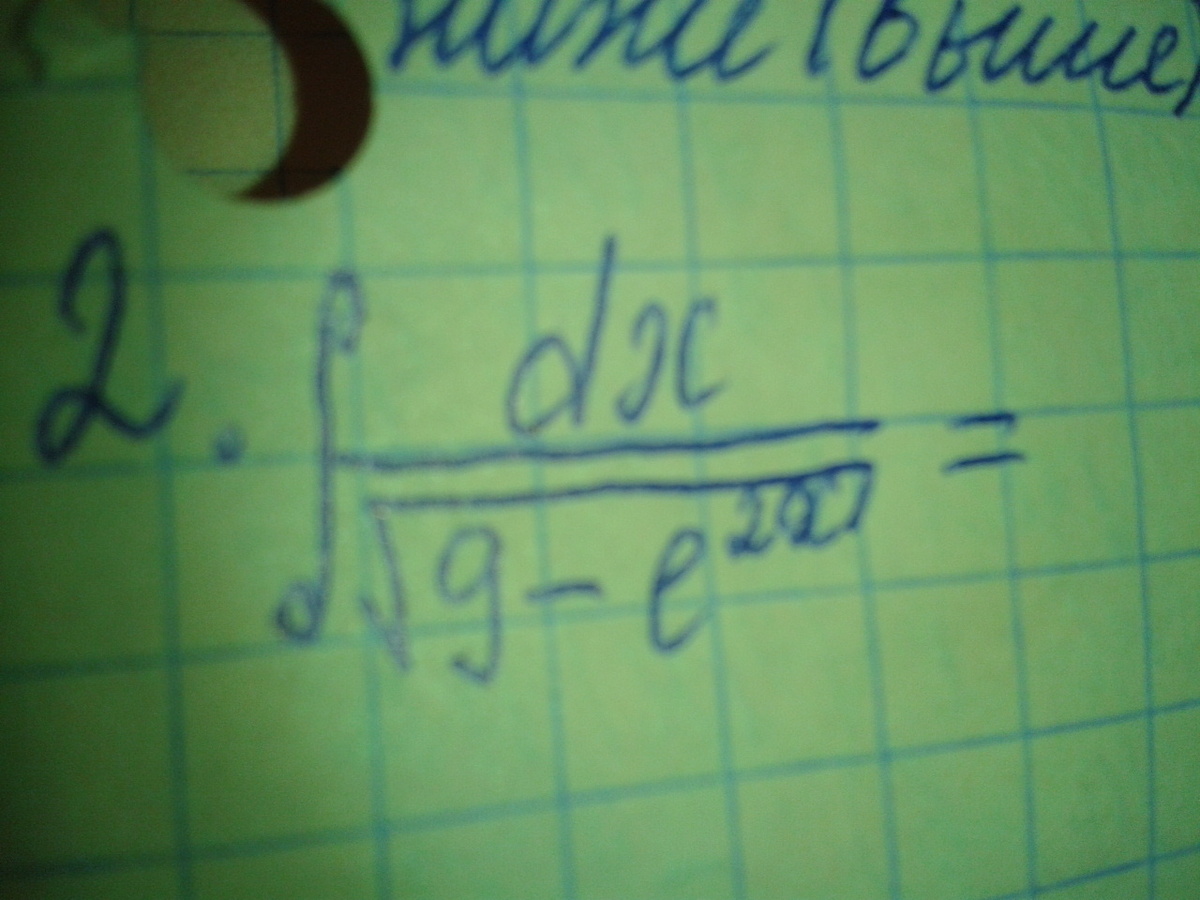
Ответы
Автор ответа:
0
Int dx / √(9 - e^(2x)) = Int dx / [3√(1 - e^(2x)/9)] = 1/3*Int dx / √(1 - (e^x / 3)^2)
Замена e^x / 3 = t, e^x = 3t, x = ln(3t) = ln 3 + ln t, dx = dt / t
1/3*Int dt / [t*√(1 - t^2)] = 1/3*(-1)*ln |(1 + √(1 - t^2) ) / t| =
= -1/3*ln |[1 + √(1 - e^(2x)/9)] / (e^x / 3)| + C = -1/3*ln |[3 + √(9 - e^(2x))] / e^x| + C =
= -1/3*[ ln | 3 + √(9 - e^(2x)) | - ln e^x] + C = -1/3*[ ln | 3 + √(9 - e^(2x)) | - 1] + C
Замена e^x / 3 = t, e^x = 3t, x = ln(3t) = ln 3 + ln t, dx = dt / t
1/3*Int dt / [t*√(1 - t^2)] = 1/3*(-1)*ln |(1 + √(1 - t^2) ) / t| =
= -1/3*ln |[1 + √(1 - e^(2x)/9)] / (e^x / 3)| + C = -1/3*ln |[3 + √(9 - e^(2x))] / e^x| + C =
= -1/3*[ ln | 3 + √(9 - e^(2x)) | - ln e^x] + C = -1/3*[ ln | 3 + √(9 - e^(2x)) | - 1] + C
Похожие вопросы
Предмет: Химия,
автор: homuskuangur75
Предмет: Геометрия,
автор: viktoriya2301
Предмет: Английский язык,
автор: serafingaiduk01
Предмет: Информатика,
автор: joa
Предмет: Литература,
автор: istarskrim