Предмет: Алгебра,
автор: Аноним
Докажите равенство (4+\sqrt(15))*(\sqrt(10)-\sqrt(6))*\sqrt(4-\sqrt(15))=2 Решение полностью, пожалуйста
Даю 50 Баллов
(4+√15)*(√10-√6)*√(4-√15)=2
Kristinamelaa:
мне кажется ты допустил ошибку когда переписывал пример, скинь фото примера
Ответы
Автор ответа:
2
Ответ:
Объяснение
**************************************
Приложения:
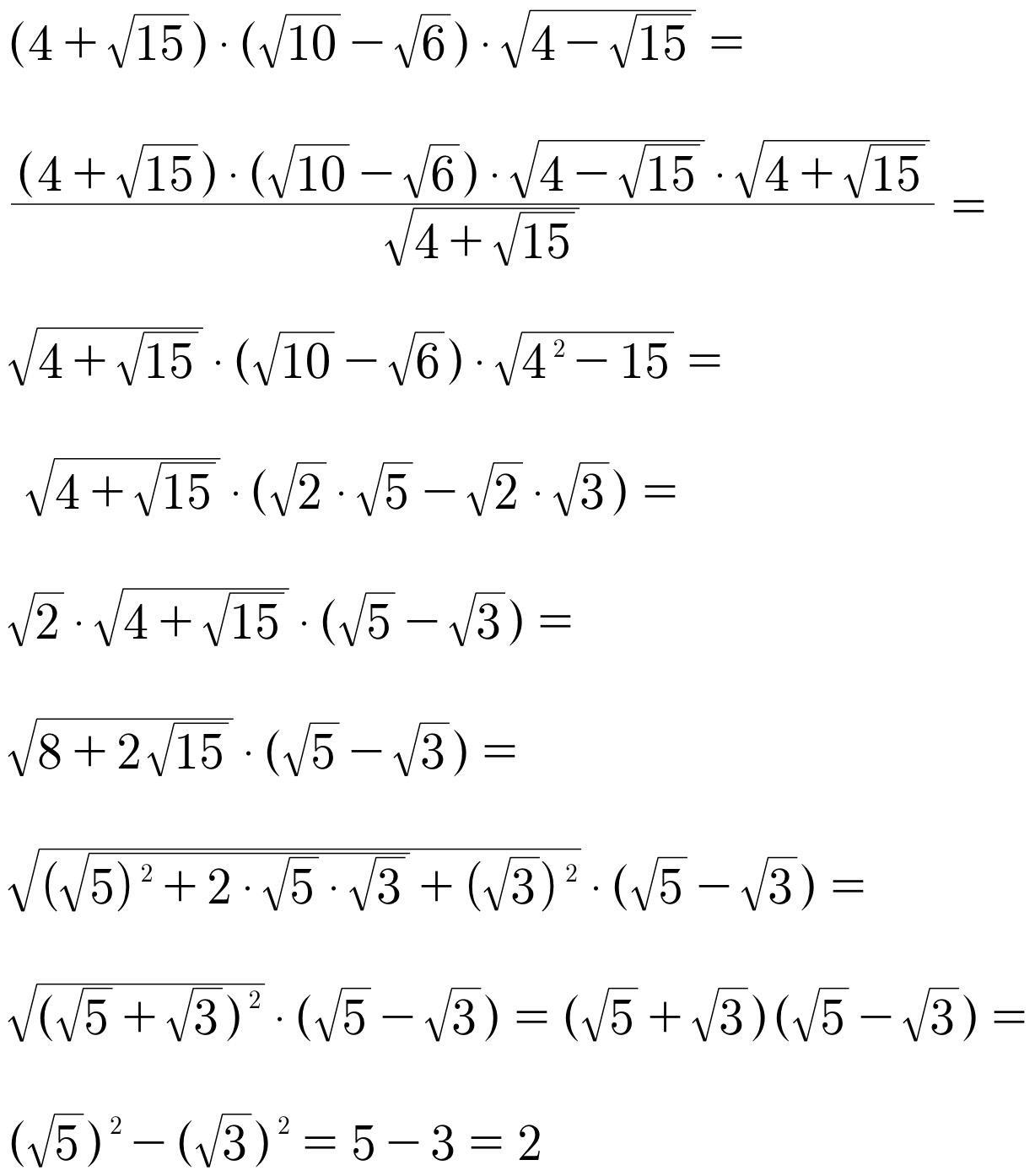
Автор ответа:
0
Помогите пожалуйста решить дроби подробно Алгебра
https://znanija.com/task/37899784?utm_source=android&utm_medium=share&utm_campaign=question
https://znanija.com/task/37899784?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Английский язык,
автор: uradovs
Предмет: Қазақ тiлi,
автор: abdulla102
Предмет: Английский язык,
автор: svirina6nastya
Предмет: География,
автор: Viktoroz
Предмет: Математика,
автор: maryana2002kisa