Предмет: Геометрия,
автор: aaa444a4a40
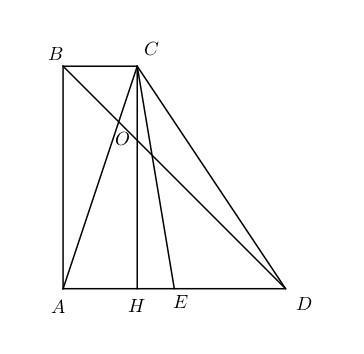
Есть прямоугольная трапеция ABCD, AD параллельно BC угол A = угол B = 90* AB=AD=4 AC пересекает BD в точке О отношение BO к OD = 1 к 3 (BO/OD=1/3) найти CE,где E - середина AD
aaa444a4a40:
помогите пожалуйста(((
AB = AD = 4? Уверены, что большое основание равен меньшей боковой стороны?
здравствуйте,да
могу прикрепить условие
именно оригинал
Ответ есть?
нету
если вы решите не решать,скажите это,пожалуйста
Знаю
Ответы
Автор ответа:
2
как накрест лежащие при
и секущей
как вертикальные.
(по двум углам). Из подобия треугольников следует пропорциональность соответствующих сторон.
Поскольку — середина
, то
. Проведём
, тогда
.
По теореме Пифагора из
Приложения:
мое уважение!
Похожие вопросы
Предмет: Русский язык,
автор: pnkratovo
Предмет: Другие предметы,
автор: Аноним
Предмет: Українська мова,
автор: arturssas
Предмет: Алгебра,
автор: лера783477
Предмет: Алгебра,
автор: bobo2662