Предмет: Алгебра,
автор: Filka7
Задание номер 4 Найти производную функции
Приложения:
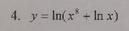
Ответы
Автор ответа:
1
Автор ответа:
1
производная сложной функции, внешняя - логарифмическая, зависит от суммы степенной и логарифмической. Поэтому схема нахождения производной функции у=㏑v, найти производную логарифма и умножить на производную v=x⁸+㏑x, т.к.
у'=(1/v)*v'
у'=1/(x⁸+㏑x)*(x⁸+㏑x)'=(8х⁷+(1/х))/(x⁸+㏑x);
Не четко виден знак. если в скобках минус,ТО ОТВЕТ ТАКОЙ
у'=(1/v)*v'
у'=1/(x⁸-㏑x)*(x⁸-㏑x)'=(8х⁷-(1/х))/(x⁸-㏑x);
Похожие вопросы
Предмет: Другие предметы,
автор: olgamihaylova
Предмет: Русский язык,
автор: MandarinXD
Предмет: Русский язык,
автор: kuzu13
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: Kateysh1