Question

Помогите пожалуйста, нужно ответить в течение часа
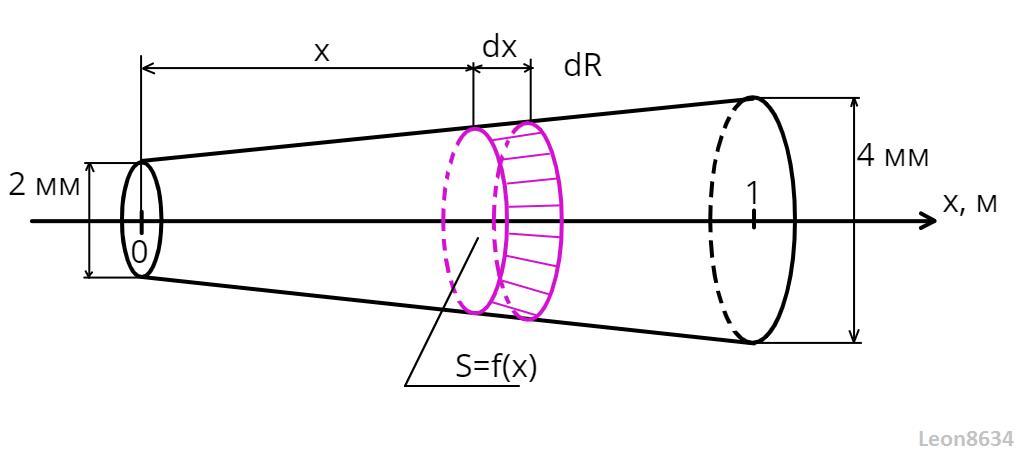
Определить сопротивление нихромового проводника, если он преставляет собой усеченный конус с диаметрами оснований 2 и 4 мм, высотой 1 м. Подводящие провода подключены к основаниям конуса. Удельное сопротивление нихрома принять равным 10^-6 Ом*м.

Answer 1

Ответ:

0,16 Ом

Объяснение:

Разобьем проводник на элементарные элементы длинной dx и площадью S(x) очевидно, сопротивление одного того элемента равно:

$\displaystyle dR=\rho\frac{dx}{S(x)}$

Установим вид функции S(x). Зависимость радиуса проводника от его длины представляет линейную функцию вида y=kx+b, найдем ее коэффициенты решив следующую СЛУ:

$\displaystyle k*0+b=10^{-3}$

$\displaystyle k*1+b=2*10^{-3}$

Откуда b=10⁻³, k=10⁻³

Таким образом $\displaystyle r(x)=10^{-3}x+10^{-3}$

Площадь поперечного сечения проводника:

$\displaystyle S(x)=\pi r^2(x)=\pi (10^{-3}x+10^{-3})^2=10^{-6}\pi (x+1)^2$

Сопротивление всего проводника найдем как предельную сумму сопротивлений его элементарных длин (они соединены последовательно):

$\displaystyle R=\int\limits^1_0 {} \, dR =\frac{\rho}{10^{-6}\pi } \int\limits^1_0 {\frac{dx}{(x+1)^2} }$

Берем интеграл:

$\displaystyle R=-\frac{\rho}{10^{-6}\pi }* \frac{1}{x+1} |_0^1=-\frac{\rho}{10^{-6}\pi } *\frac{1}{2}+\frac{\rho}{10^{-6}\pi } =\frac{\rho}{2*10^{-6}\pi }$

Выполним расчет:

$\displaystyle R=\frac{10^{-6}}{2*10^{-6}*\pi } =\frac{1}{2\pi } \approx0.16$ Ом.