Предмет: Физика,
автор: duvgsdsdf
Решите задачку по физике срочно. Во вложении
Приложения:
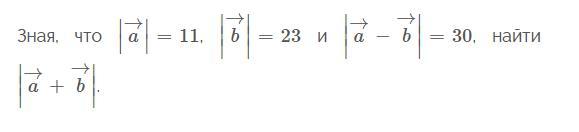
braincracker:
не понятно почему по физике)
ну так векторы же
Ответы
Автор ответа:
0
Ответ:
20
Объяснение:
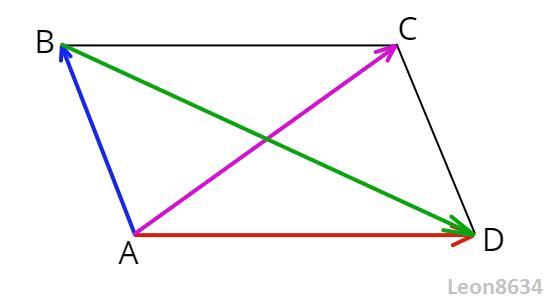
Просто вспомним правило параллелограмма (см. рисунок). Очевидно, что ,
,
, тогда искомый модуль суммы равен длине второй диагонали АС, найти ее можно, воспользовавшись тождеством параллелограмма:
.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: simonov2004
Предмет: Русский язык,
автор: светабик
Предмет: Русский язык,
автор: imperotriza
Предмет: История,
автор: dariamartfun