Предмет: Геометрия,
автор: Аноним
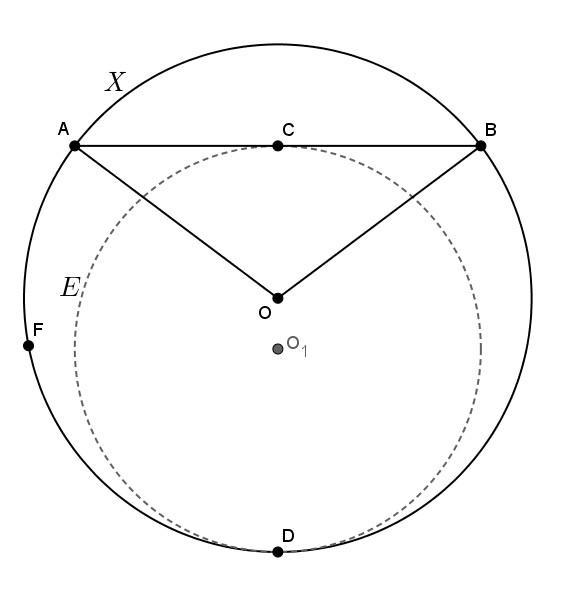
В окружности X проведены хорда AB и вторая окружность E, которая касается хорды AB и окружности X в точках C и D . Докажите, что прямая CD содержит середину одной из дуг окружности X с концами A, B.
Ответы
Автор ответа:
3
См. рисунок.
Обозначим центр малой окружности через . Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке:
.
Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка — середина хорды
. Треугольник
равнобедренный (поскольку отрезки
и
равны как радиусы). Значит, медиана
является также и высотой. Получим, что
. Учитывая предыдущее равенство, получим, что
. Это значит, что точки
и
лежат на одной прямой. Тогда на той же прямой лежит точка касания
(ведь по условию она диаметрально противополож
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: birossa
Предмет: Русский язык,
автор: рамрамрпамр
Предмет: Русский язык,
автор: remevelina17
Предмет: Математика,
автор: 3037
Предмет: История,
автор: Юмас