Question

Висота паралелограма, довжина якої 24 см, опущена на більшу
сторону і ділить її на відрізки 7 і 32 см, починаючи від вершини гострого
кута. Обчисліть периметр і меншу діагональ паралелограма.
​

Answer 1

Объяснение:

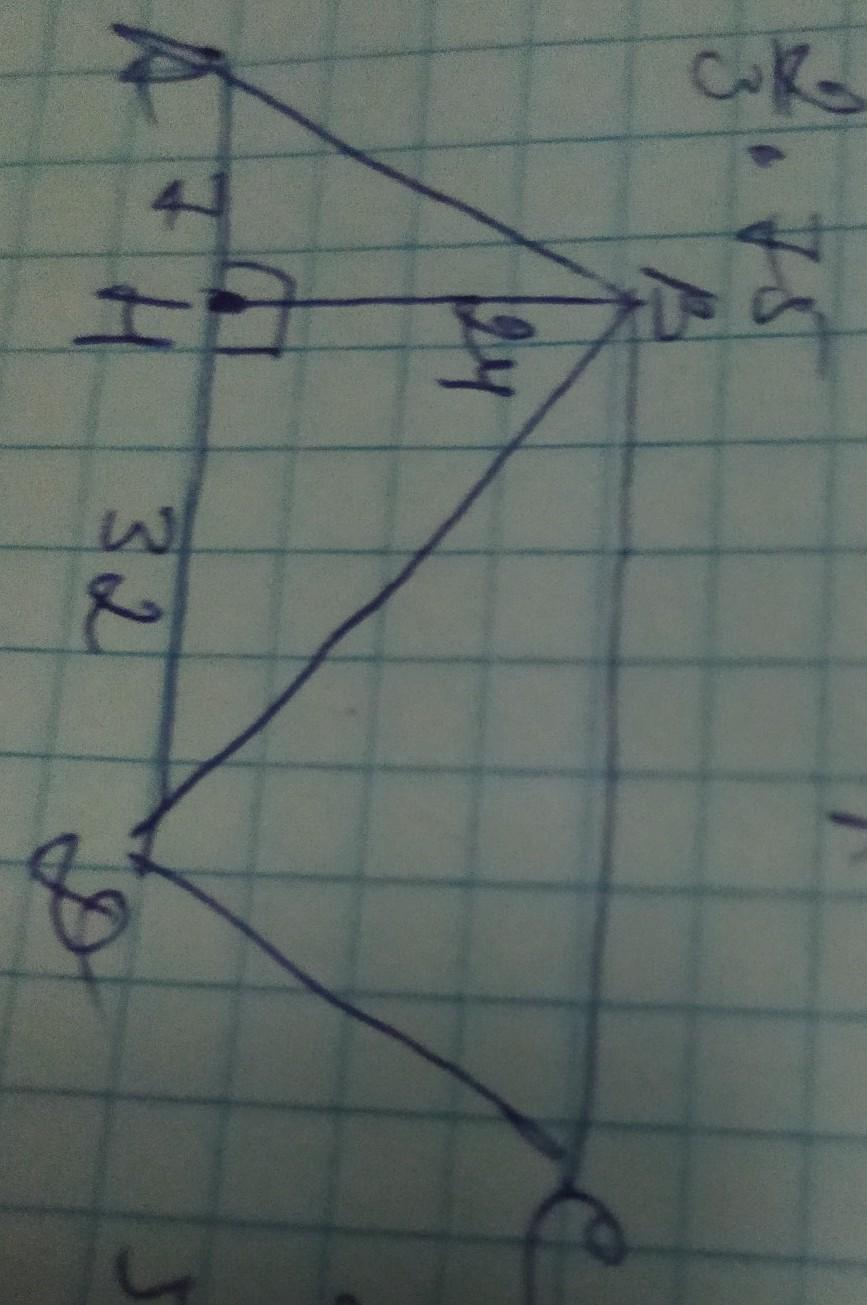
обозначим вершины параллелограмма А В С Д с высотой ВН и меньшей диагональю ВД. Высота ВН и диагональ ВД, образуют 2 прямоугольных треугольника АВН и ВДН, в которых ВН, АН, ДН - катеты, а АВ и ВД - гипотенузы. По теореме Пифагора найдём диагональ ВД в ∆ВДН:

ВД²=ВН²+АД²=24²+32²=576+1024=1600; ВД=√1600=40см

Также найдём АВ из ∆АВН:

АВ²=ВН²+АН²=24²+7²=576+49=625; АВ=√625=25см

АВ=СД=25см

АД=ВС=7+32=39см

Теперь найдём периметр параллелограмма зная его стороны: 2×25+2×39=50+78=128см

ОТВЕТ: Р=128 см, ВД=40см