Question

Помогите пожалуйста решить задачу по геометрии. НУЖНО ПОДРОБНОЕ РЕШЕНИЕ. Фото прикреплено.

Answer 1

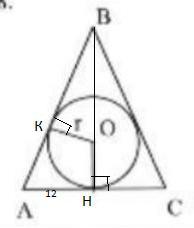
В равнобедренный треугольник АВС , АВ=ВС=15 , АС=24, вписана окружность (О; r). Найдите r.

Объяснение:

1)Пусть ВН ⊥АС. Центр вписанной окружности О лежит в точке пересечения биссектрис. В равнобедренном треугольнике биссектриса совпадает с высотой ⇒поэтому О лежит на высоте ВН.

АН=42 :2=12( т.к. ВН и медиана ) . Будем искать r  из ΔКВО.

2) ΔАВН-прямоугольный, по т. Пифагора ВН=√(15²-12²)=9. Тогда отрезок ВО можно выразить так ВО=9-r.

По свойству отрезков касательных АН=АК=12⇒КВ=15-12=3.

3)  ΔКВО-прямоугольный , по свойству радиуса , проведенного в точку касания . По т. Пифагора ВО²=ОК²+КВ²

(9-r)²=r²+3²  ,81-18r+r²=r²+9  ,18r=72 , r=4 .