Предмет: Алгебра,
автор: datrofimova
Плиииз помогите очень очень нужно
Приложения:
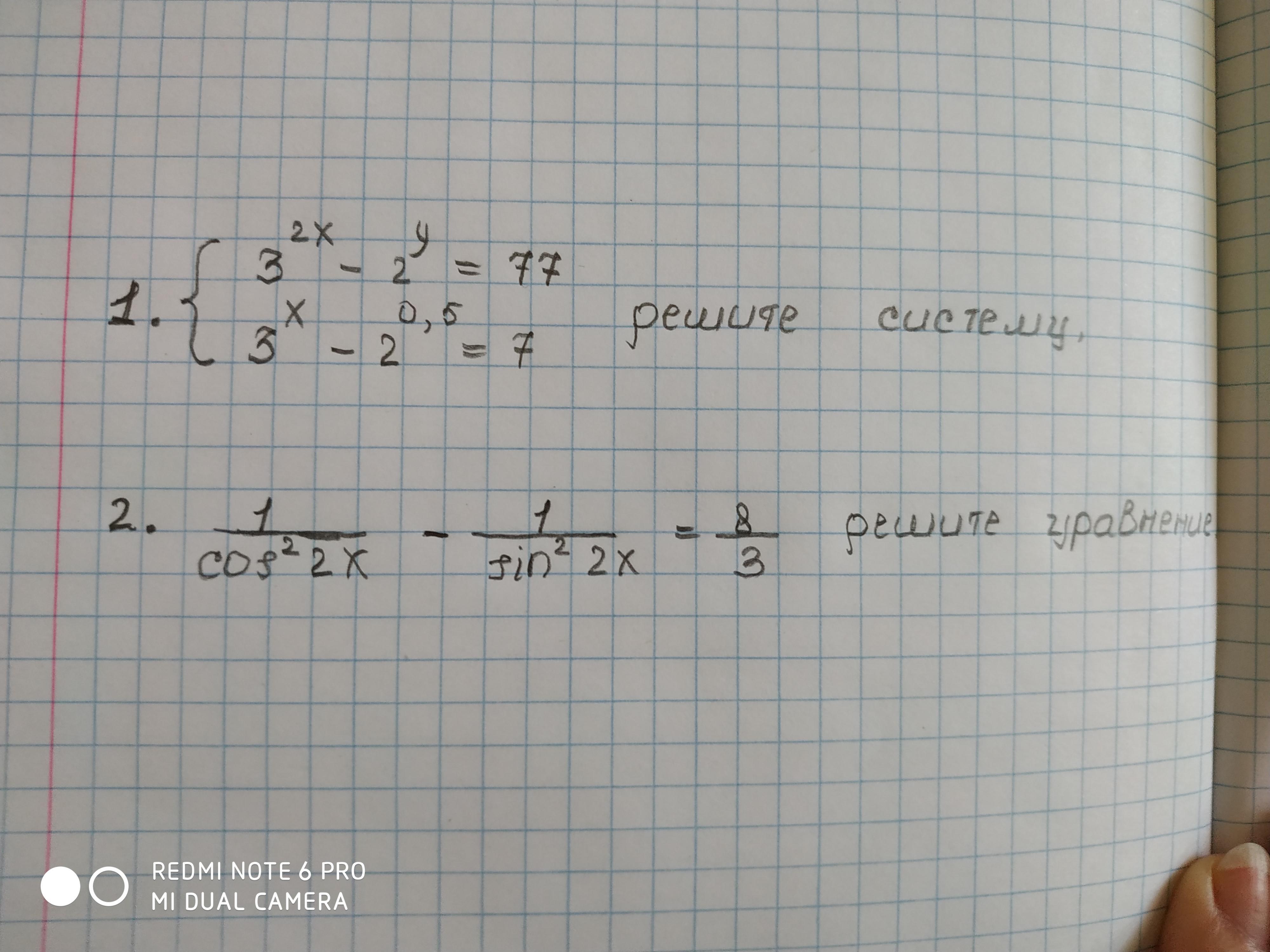
nafanya2014:
во втором уравнении системы степень 2^(0,5) написано верно? точно нет у???
Есть
Извините, я пропустила у
Ответы
Автор ответа:
1
1.
Замена переменной: ;
Тогда
;
Решаем систему:
⇒
Применяем способ сложения: одно из уравнение системы заменим суммой двух уравнений.
Обратный переход: ;
О т в е т. (2;2)
2.
и
Так как
Биквадратное уравнение:
или
9 уравнение не имеет корней, т.к
или
или
или
О т в е т.
Похожие вопросы
Предмет: Английский язык,
автор: Lera200325
Предмет: Русский язык,
автор: lhfrjif82004
Предмет: Английский язык,
автор: katya21042003
Предмет: История,
автор: pravdovichkaay
Предмет: Химия,
автор: Аноним