Предмет: Геометрия,
автор: os356034
Доказать, что биссектрисы двух углов с соответственно перпендикулярными сторонами парралельны, принадлежат одной прямой или взаимно перпендикулярны. все варианти я решил(а), но меня интересует вариант принадлежат одной прямой. Нужно доказательство именно этого варианта
os356034:
нужно сегодня
дам лучший первому
если решите можете еще и тут написать (+ 18 халявних балов) https://znanija.com/task/37840160
спасибо
Ответы
Автор ответа:
5
" Доказать, что биссектрисы двух углов с соответственно перпендикулярными сторонами парралельны, принадлежат одной прямой или взаимно перпендикулярны. все варианти я решил(а), но меня интересует вариант принадлежат одной прямой. Нужно доказательство именно этого варианта "
Объяснение:
Данные углы образуют четырехугольник, противоположные углы которого в сумме дают 180°.
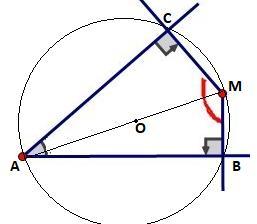
Пусть для определенности МС⊥АС, МВ⊥АВ и АМ- биссектриса ∠САВ . Тогда около 4-х угольника АВМС можно описать окружность , т.к. ∠АСМ+∠АВМ=180° и АМ-диаметр .
Т.к. МС⊥АС, МВ⊥АВ , то М- равноудалена от сторон АС и АВ ∠САВ . Тогда ΔАСМ=ΔАВМ как прямоугольные по катету и гипотенузе⇒ соответственные элементы равны ⇒∠СМА=∠АВМ⇒ МА биссектриса ∠СМВ.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: mafiarulees
Предмет: Русский язык,
автор: Алеха22
Предмет: Русский язык,
автор: 79042840046
Предмет: Геометрия,
автор: 42fas
Предмет: Алгебра,
автор: kkalinina904