Предмет: Физика,
автор: vingerov3
Небольшой шарик на нити движется по окружности в вертикальной плоскости. Найти массу шарика, если максимальное натяжение нити на ΔF=2,35 Н больше минимального.
Ответы
Автор ответа:
8
Ответ:
39 г
Объяснение:
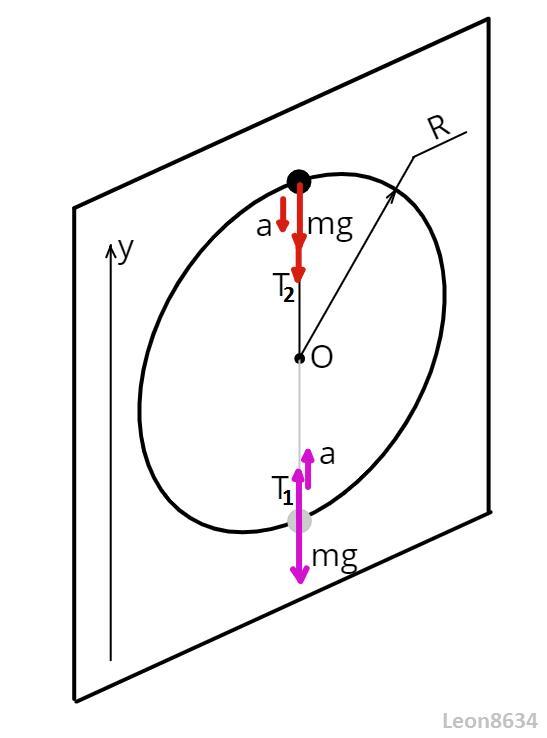
Пусть шарик вращается равномерно. Очевидно, наибольшего/наименьшего значения натяжение нити достигает в нижней/верхней точках траектории. Распишем втором закон Ньютона в проекции на вертикальную ось в этих точках (обязательно учтем, что скорость шарику внизу больше на величину , где H=2R):
Выразим отсюда натяжения нитей:
Их разность:
Откуда, искомая масса:
кг или 39 г.
Приложения:
vingerov3:
Неверно. Разность квадратов скоростей не равно нулю, т.к. линейная скорость в нижней точке больше чем в верхней точке (так как действует сила тяжести). Эту разность скоростей нужно находить из закона сохранения энергии, в итоге она получается равна 4mg, подставляем в формулу разности натяжения нити получаем 6mg=ΔF, откуда m=39мг.
Ну конечно неверно! Совсем зарешался... Не учел ЗСЭ, попрошу модераторов отправить на исправление...
Похожие вопросы
Предмет: Русский язык,
автор: Angel10072001
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Айдар123
Предмет: Математика,
автор: Bubbca
Предмет: Математика,
автор: Katyasant