Question

50 БАЛЛОВ. Хелп, задача из ЕГЭ по профильной математике.

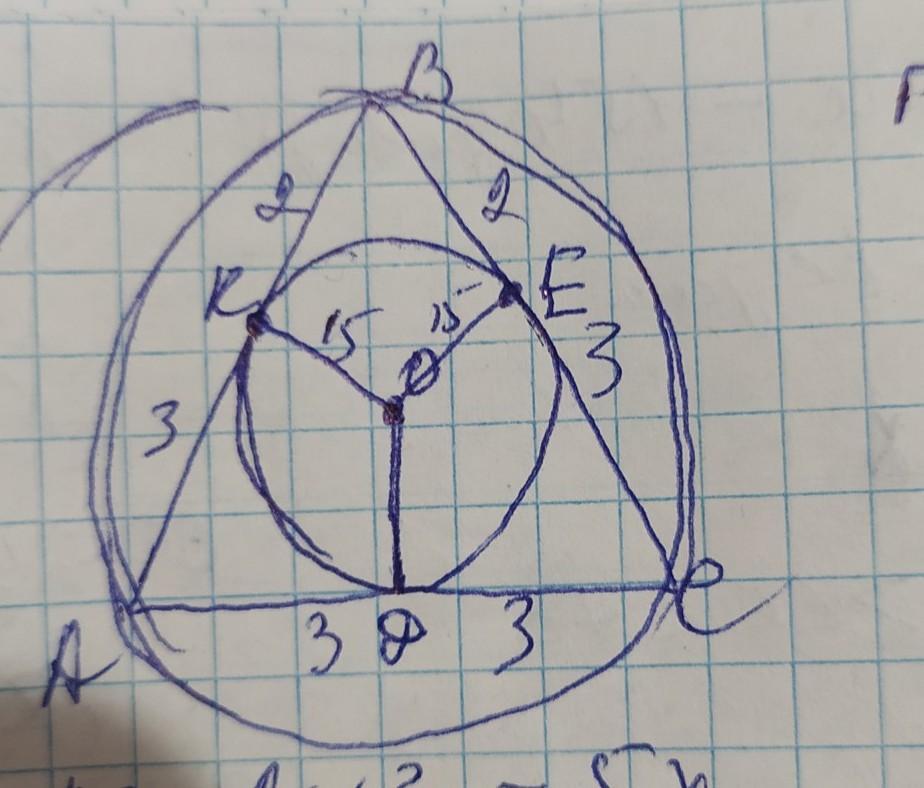
Окружность радиусом 15, вписанная в равнобедренный треугольник, делит боковую сторону этого треугольника в отношении 2:3, считая от вершины основания. Во сколько раз длина окружности, описанной около этого треугольника, превосходит число π?​

Answer 1

Ответ:

в 62,5 раз

Объяснение:

обозначим вершины треугольника А В С с основанием АС, центром вписанной окружности О, а точки касания окружности со сторонами треугольника К Е Д, а отношение отрезков стороны как 2х и 3х. Так как ∆АВС равнобедренный, то АВ=ВС и ВЕ/ЕС=2/3. Стороны треугольника являются касательными к вписанной окружности и касательные, соединяясь в одной вершине равны от вершины до точки касания, поэтому ВК=ВЕ=2х, АК=АД=3х, ЕС=СД=3х. Итак: стороны треугольника составят:

АВ=ВС=2х+3х=5х

АС=3х+3х=6х

Теперь найдём стороны треугольника используя формулу нахождения радиуса вписанной окружности. Составим уравнение:

$\frac{ac}{2} \times \sqrt{ \frac{2ab - ac}{2ab + ac} } = r$

$\frac{6x}{2} + \sqrt{ \frac{2 \times 5x - 6x}{2 \times 5x + 6x} } = 15$

$3x \times \sqrt{ \frac{10x - 6x}{10x + 6x} } = 15$

$3x \times \sqrt{ \frac{4x}{16x} } = 15$

$3x \times \frac{2}{4} = 15$

3x×0,5=15

1,5x=15

x=15÷1,5=10

Тогда стороны треугольника составят:

АВ=ВС=5×10=50

АС=6×10=60

Теперь найдём радиус описанной окружности, зная стороны треугольника по формуле:

R=

$\frac{ab {}^{2} }{ \sqrt{(2ab) {}^{2} - ac {}^{2} } }$

$\frac{50 {}^{2} }{ \sqrt{(2 \times 50) {}^{2} - 60 {}^{2} } } = \frac{2500}{ \sqrt{100 {}^{2} - 3600} } = \frac{2500}{ \sqrt{10000 - 3600} } = \frac{2500}{ \sqrt{6400} } = \frac{2500}{80} = 31.25$

Итак: радиус описанной окружности R=31,25 и теперь найдём длину окружности по формуле: L=2πR=

=2π×31,25=62,5π;

Чтобы узнать во сколько раз длина описанной окружности превосходит число π, нужно полученный результат разделить на π:

62,5π÷π=62,5