Предмет: Алгебра,
автор: lolilollil
решите, пожалуйста. спасибо большое
Приложения:
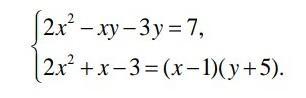
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ashubasar03
Предмет: Русский язык,
автор: marina881
Предмет: Другие предметы,
автор: abdulkerimovka
Предмет: Математика,
автор: Katenka5834