Предмет: Алгебра,
автор: sheldon2332
Помогите пожалуйста, найти предел
Приложения:
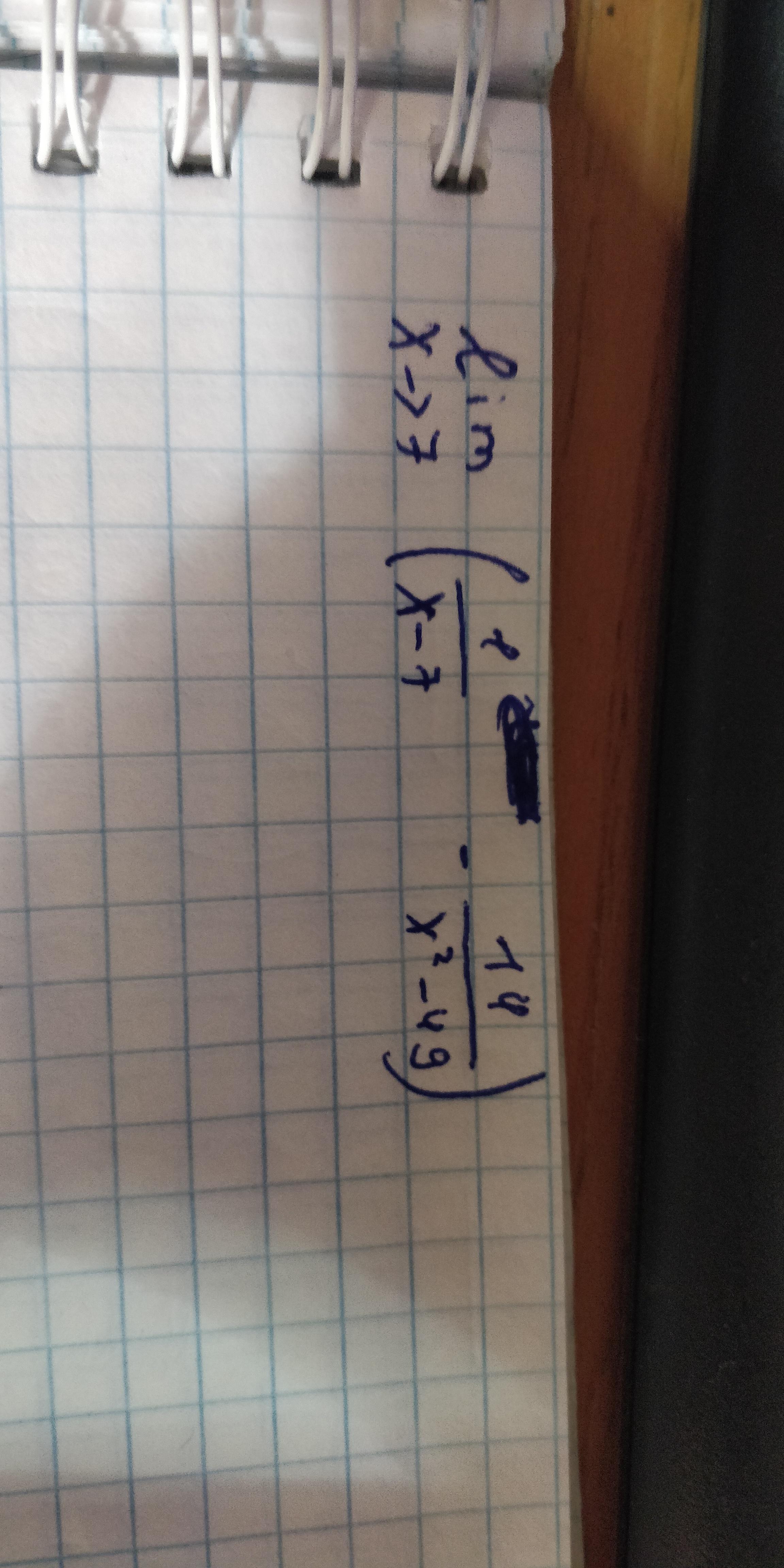
Ответы
Автор ответа:
0
преобразуем выражение
1/(x - 7) - 14/(x² - 49) = (x + 7)/(x - 7)(x + 7) - 14/(x - 7)(x+7) = (x + 7 - 14)/(x - 7)(x + 7) = 1/(x + 7)
lim(x->7) ( 1/(x - 7) - 14/(x² - 49) ) = lim(x->7) 1/(x + 7) = 1/(7 + 7) = 1/14
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Desgan
Предмет: Русский язык,
автор: svetakh
Предмет: Русский язык,
автор: tanywahrina
Предмет: Биология,
автор: vipangel2019
Предмет: Математика,
автор: оленька117