Предмет: Алгебра,
автор: darkripper111
тема інтеграли та ряди
Приложения:

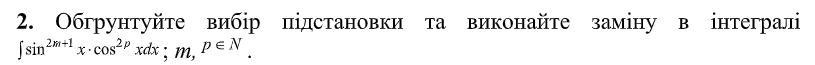
Ответы
Автор ответа:
0
Отметим что при всех n члены ряда положительны
Далее
То есть ряд
является мажорантным для нашего. Но он сходится, тк это бесконечно убывающая геометрическая прогрессия.
Значит сходится и исходный ряд
Автор ответа:
0
Применим признак Коши в предельной форме, а именно Если существует предел корня энной степени из aₙ при n стремящемся к бесконечности, и равен λ, то при λ<1 ряд сходится, приλ >1 расходится, при λ=1 может как сходиться, так и расходиться.
Корень энной степени из aₙ равен (3n²-1)/(7n²+4), этот предел равен отношению коэффициентов при одинаковых высших степенях n, т.е. 3/7, а, следовательно, ряд сходится.
Похожие вопросы
Предмет: Русский язык,
автор: letsek
Предмет: Английский язык,
автор: pet1331
Предмет: Русский язык,
автор: Ксюфи
Предмет: Математика,
автор: 1rina03
Предмет: Математика,
автор: enzochaly