Question

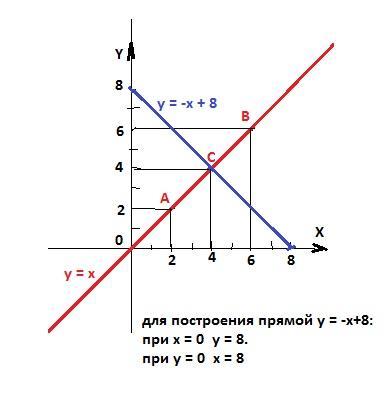
Даны точки A(2; 2) и B(6; 6). Пусть точка C

− середина отрезка AB. Составьте

уравнение прямой, перпендикулярной

прямой AB и проходящей через точку C.​

Answer 1

Ответ:

y = -x +8.

Объяснение:

Координаты середины отрезка: С((2+6)/2;(2+6)/2) или С(4;4).

Уравнение прямой АВ  формуле:

(x-x1)/(x2-x1) = (y-y1)/(y2-y1) или  

(x-2)/(6-2) = (y-2)/(6-2)  =>  y = x.

Итак, уравнение прямой АВ имеет вид  y = kx, где k = 1.

Условие перпендикулярности прямых:

k1 = -1/k, то есть все прямые, перпендикулярные прямой АВ будут иметь уравнение y = -x.

Нас интересует только одна прямая - проходящая через точку С(4;4).

Найдем уравнение этой прямой по формуле:

Y - Yc = -(X - Xc) или

y - 4 =  -x + 4  =>  y = -x +8.