Предмет: Математика,
автор: xsl
Помогите пожалуйста решить. Задание на фото.
Приложения:
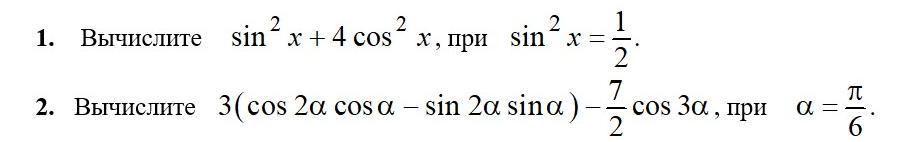
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ:
1) 2.5
2) 0
Пошаговое объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: dmi7558
Предмет: Другие предметы,
автор: nsaratovskaya13
Предмет: Русский язык,
автор: dflbv20050102
Предмет: История,
автор: arinakoltunova01
Предмет: Математика,
автор: яниник