Question

Решите задания 5,6,7 как можно быстрее

Answer 1

Объяснение: см. во вложении

Объяснение концовки последнего примера. Большему значению аргумента соответствует меньшее значение функции, т.к. функция при х∈[2;+∞) убывает.

Answer 2

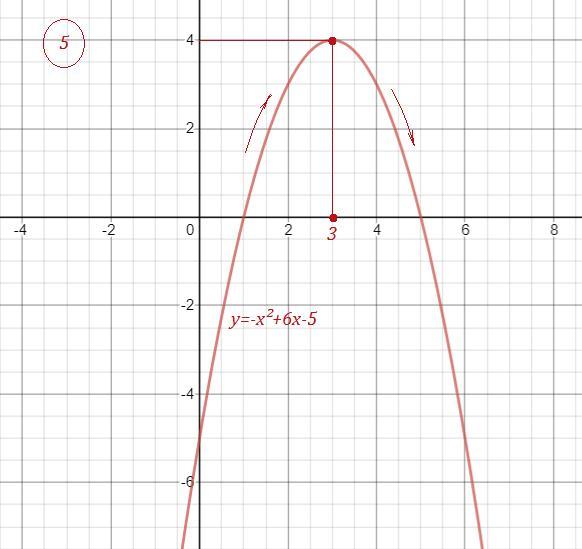
5)   $y=-x^2+6x-5$

 Абсцисса вершины параболы :  $x_{v}=-\dfrac{b}{2a}=\dfrac{-6}{-2}=3$  .

Функция возрастает при  $x\in (\infty \, ;\, 3\, ]$   и убывает при   $x\in [\ 3\, ;+\infty )\ .$

$6)\ \ y=x^2-4\\\\(x-2)(x+2)>0\ \ \to \ \ \ x\in (-\infty \, ;-2)\cup (\, 2\, ;+\infty )$

$7)\ \ f(x)=-4x^2+16x-3\\\\x_{versh.}=-\dfrac{b}{2a}=\dfrac{-16}{2\cdot (-4)}=2$

Так как а= -4<0 , то ветви параболы направлены вниз и на промежутке

$[\ 2\, ;\, +\infty )$  функция убывает. Поэтому при   $x_1<x_2$  значения функции связаны соотношением  $f(x_1)>f(x_2)\ .$  Тогда имеем:

$2<5<8,1<11,8\ \ \ \Rightarrow \ \ \ f(2)>f(5)>f(8,1)>f(11,8)$  .