Question

Тема: перпендикулярность плоскостей. 1) Докажите, что пересекающиеся грани прямоугольного параллелепипеда перпендикулярны. 2) Докажите, что плоскости диагональных сечений AB1 C1 D и BA1 D1 C куба A…D1 перпендикулярны.

Answer 1

1) Докажите, что пересекающиеся грани прямоугольного параллелепипеда перпендикулярны. 2) Докажите, что плоскости диагональных сечений AB1 C1 D и BA1 D1 C куба A…D1 перпендикулярны.

Объяснение:

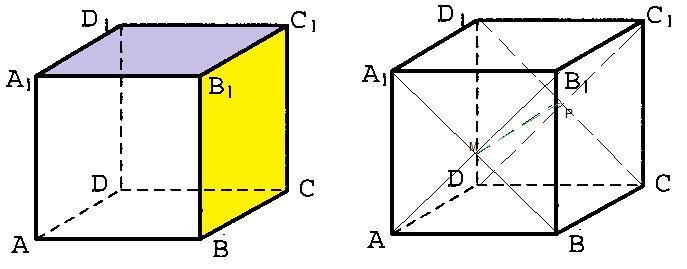
1)Две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы. Выберем для определенности плоскости   ( А₁В₁С₁) и (ВВ₁С).

В₁С₁ -линия пересечения плоскостей ( А₁В₁С₁) и (ВВ₁С).

Д₁С₁ ⊥  В₁С₁  и СС₁⊥ В₁С₁ , т.к. все грани прямоугольного параллелепипеда -прямоугольники⇒ ( А₁В₁С₁) ⊥ (ВВ₁С).

2)Все грани куба-квадраты. Диагонали квадрата  взаимно -перпендикулярны . МР ,линия пересечения граней  (AB₁C₁D) и (BA₁D₁С) . Значит линейный угол данного двугранного ∠АМВ=90° ⇒данные плоскости перпендикулярны.