У прямокутному трикутнику гострі кути відносяться як 1:2. Більший катет дорівнює 4 корінь з 3 см. Знайти площу круга, описаного навколо даного трикутника
Ответы
Ответ:
Sокр.=16π=50,24 см²
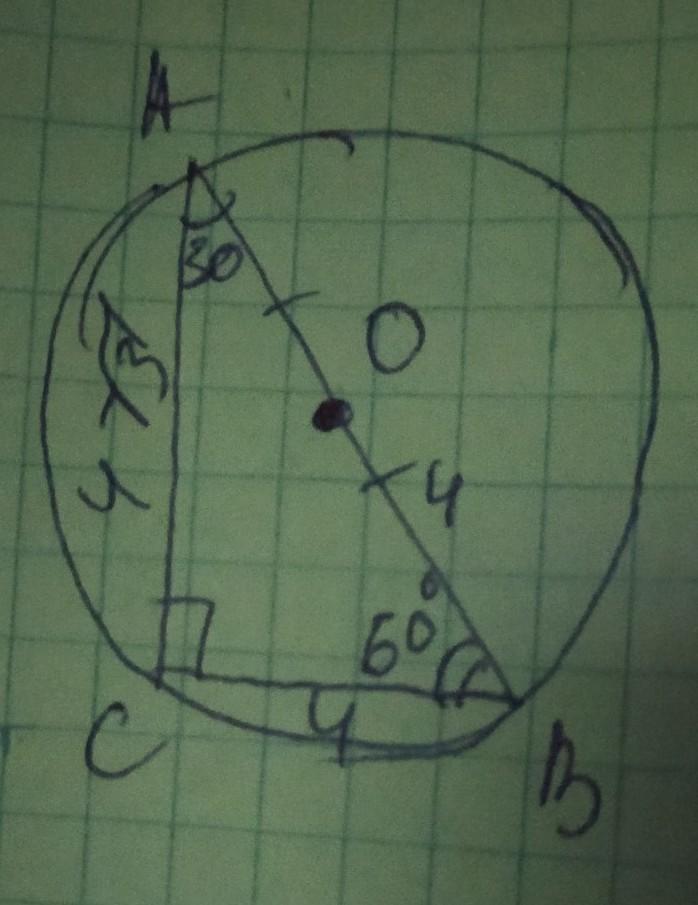
Объяснение: обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ, центр окружности О, а соотношение 1:2 как х и 2х и так как сумма острых углов прямоугольного треугольника составляет 90°, составим уравнение:
х+2х=90
3х=90
х=90÷3=30°.
Итак: меньший острый угол А=30°, тогда второй острый угол В=2×30=60°
Большая сторона лежит напротив большего угла и меньшая сторона лежит напротив меньшего угла, поэтому больший катет АС, имеющий величину 4√3, лежит напротив угла 60°, а меньший катет ВС, будет располагаться напротив угла 30°и будет равен половине гипотенузы ( свойство угла 30°). Пусть меньший катет=у, тогда гипотенуза АВ=2у. Зная величину большего катета, составим уравнение используя теорему Пифагора:
АВ²–ВС²=АС ²
(2у)²–у²=(4√3)²
4у²–у²=16×3
3у²=48
у²=48÷3=16
у=√16=4
Итак: меньший катет ВС=4см, тогда гипотенуза АВ=2×4=8см
В прямоугольном треугольнике центр описанной окружности располагается в середине гипотенузы, поэтому радиус окружности ОА=ОВ=8÷2=4см
Площадь окружности вычисляется по формуле: πr²=π×4²=π×16=16π(см²); или 16×3,14=50,24(см²)
а – больший катет
b – меньший катет
с – гипотенуза
Решение:
1) Найдем градусные меры углов треугольника:
х+2х+90=180
3х=90
х=30° – градусная мера одного острого угла.
2×30°=60° – градусная мера второго острого угла.
90° – градусная мера третьего угла (т.к. треугольник - прямоугольный).
2) Найдём длину меньшего катета треугольника:
tgx=a/b
b=4√3/√3=4см
3) Найдём гипотенузу по теореме Пифагора:
с²=а²+b²=(4√3)²+4²=64
c=8см
4) Найдём радиус круга, описанного около данного треугольника:
R=c/2=8/2=4см
5) Найдём площадь круга:
S=пr²=3,14×4²=50,24см²
Ответ: S=50,24см²