Предмет: Физика,
автор: L7088
В сильно загрязненном водоёме толщина слоя нефти на поверхности воды составляет d=1,0 см. На поверхность водоема пустили плавать цилиндрический стакан массой m=4,0г с площадью дна S=25см2. Стакан был сначала пустым, а его дно было выше середины уровня нефти. Затем в него долили нефти так, чтобы ее уровни в стакане и снаружи сравнялись. В обоих случаях дно находилось на одном и том же расстоянии a от уровня воды. Определите плотность нефти (p1), зная что плотность воды p0= 1,0 г/см.
Приложения:
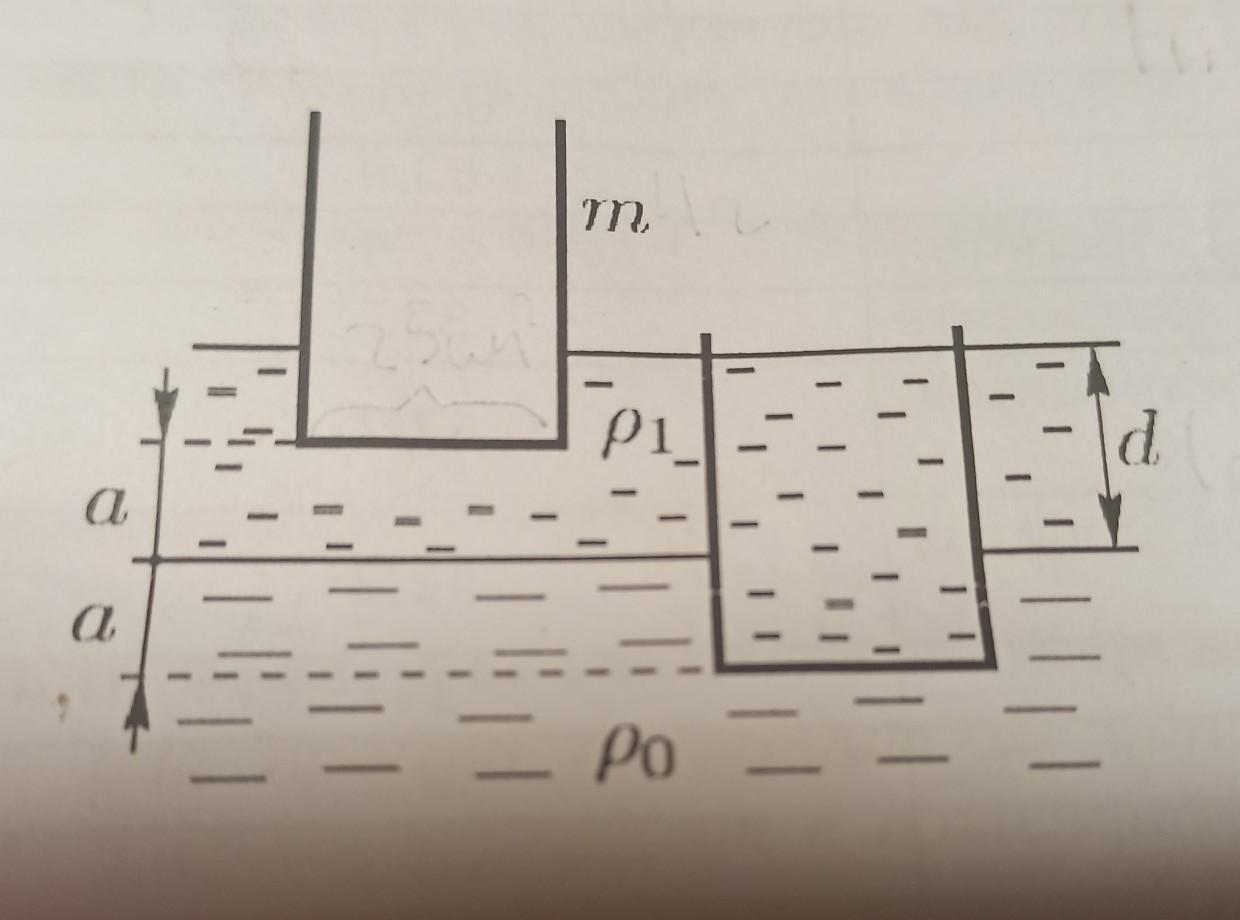
Ответы
Автор ответа:
2
Ответ:
как-то так,бери пользуйся,вроде правильно))))
Приложения:
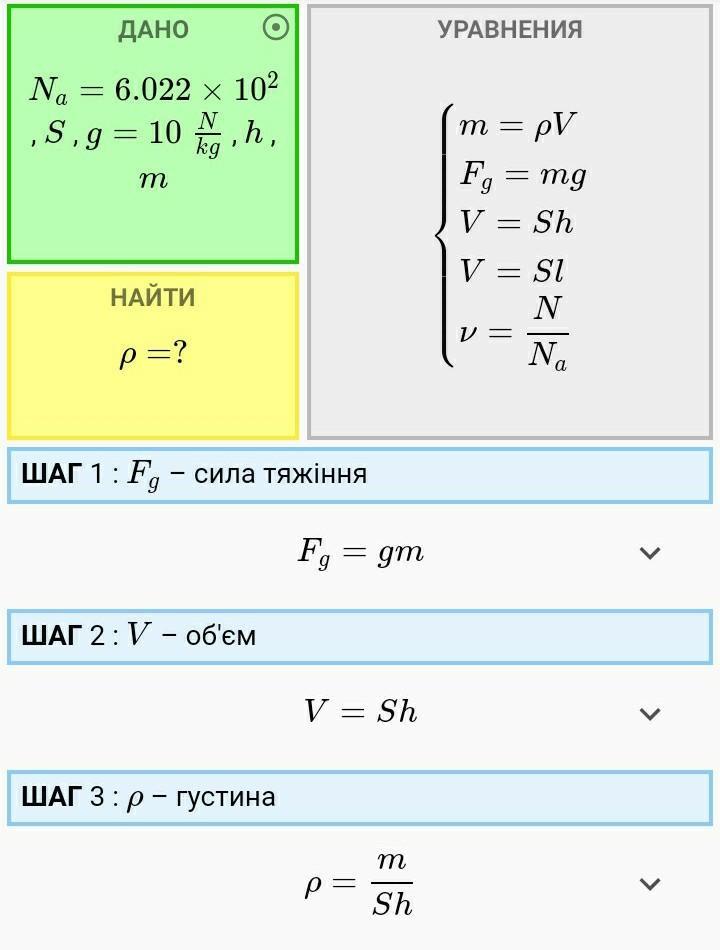
Автор ответа:
9
Ответ:
0,8 г/см³
Объяснение:
Выразим глубину погружения пустого стакана:
см
Расстояние от дна до воды:
см
После заполнения стакана:
см
По условию эти расстояния равны:
Решаем полученное квадратное уравнение:
г/см³
г/см³ - нефти с такой плотностью не существует, плотность нефти колеблется в пределах 0,73-1,04 г/см³, таким образом, искомая плотность равна 0,8 г/см³.
Похожие вопросы
Предмет: Русский язык,
автор: alona2000ua
Предмет: Русский язык,
автор: zaralakudush
Предмет: Українська мова,
автор: dacyshina1981
Предмет: Математика,
автор: M0rp3nPerfecto