Предмет: Математика,
автор: yavoitov2017
Найти все значения a, при которых имеется 2 целых решения
Приложения:
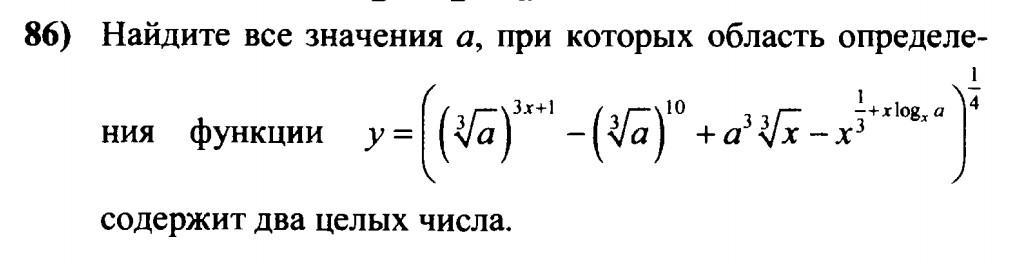
Ответы
Автор ответа:
1
Область определения задается условиями:
Так как
при
и
и
при
и
При и
значит
Показательная функция с основанием a > 1 возрастает и тогда
Такая область содержит бесчисленное множество целых значений.
Если же основание , то показательная функция убывает и
тогда
Область определения в таком случае содержит два целых числа: x=2; x=3
О т в е т.
Похожие вопросы
Предмет: Русский язык,
автор: 89658612226
Предмет: Українська мова,
автор: killalik
Предмет: Русский язык,
автор: maiiiac
Предмет: Информатика,
автор: Sasha11111111asd