Предмет: Алгебра,
автор: Shawol2
Найдите действительные решения системы уравнений
Приложения:
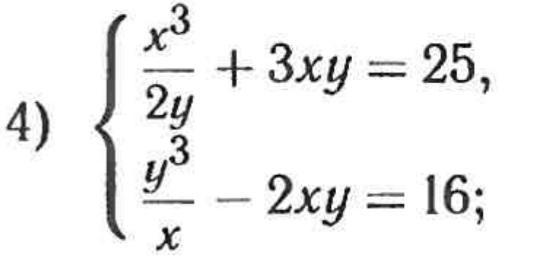
Ответы
Автор ответа:
1
Ответ: (2;4);(-2;-4)
Объяснение:
ОДЗ:
Вычитаем второе уравнение из первого:
Учитывая, что , можно поделить обе части уравнения на
:
Тут решений нет.
Похожие вопросы
Предмет: Русский язык,
автор: 111annacemenovn
Предмет: Русский язык,
автор: knyazyandavid
Предмет: Русский язык,
автор: ricaty
Предмет: Математика,
автор: МаксЯншин
Предмет: Алгебра,
автор: polinabelyaeva8