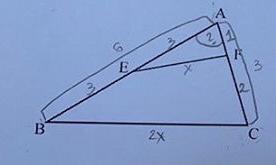
В треугольнике ABC: AB = 6см; AC = 3см; F - это точка на стороне AC, так что AF = 1см; а точка E - середина стороны AB; BC = 2EF. Вычислите угол BAC.
Ответы
Ответ:
arccos(5/12)
Объяснение:
Пусть EF=x => EF²=x²
Тогда ВС=2х => BC²=4x²
Из ΔEAF по т косинусов: EF²=EА²+FA²-2*EA*FA*cos∡BAC
=>x²=9+1-2*3*1*cos∡BAC=10-6*cos∡BAC (1)
Из ΔBAC по т косинусов: BC²=BA²+AC²-2*BA*AC*cos∡BAC
=>4x²=36+9-2*6*3*cos∡BAC =45-36*cos∡BAC (2)
Решим систему уравнений (1) и (2):
Домножим обе стороны (1) на 4. Получим
4*х²=40-24*cos∡BAC (1')
Вычтем из (2) (1')
Получим 5-12*сos∡BAC=0
cos∡BAC=5/12
=> ∡BAC = arccos (5/12)
Ответ:
<A≈65°24′
Объяснение:
как показано на рисунке пусть EF=x, a BC=2x. Рассмотрим ∆АВС и ∆AEF. У них общий угол А, который можно найти используя теорему косинусов:
из ∆AEF:
из ∆АВС:
так как угол А общий и его значение для обоих треугольников равно составим уравнение используя оба варианта:
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
6(45–4х²)=36(10–х²)
270–24х²=360–36х²
–24х²+36х²=360–270
12х²=90
х²=90÷12
х²=7,5
х=√7,5
Итак: EF=√7,5см. Теперь подставим значение х в первое уравнение:
2,5÷6≈0,4167; cos04167≈65°24′