Предмет: Математика,
автор: kamil6860
Найдите cos^2a,если sin3a/sina + cos3a/cosa =1
Приложения:
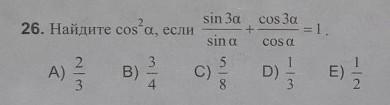
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: julia9207
Предмет: Русский язык,
автор: yanusik0203
Предмет: Русский язык,
автор: вика2224
Предмет: Химия,
автор: daniel62
Предмет: Биология,
автор: vitiukkirill