Предмет: Алгебра,
автор: Dreamcatcher579
уравнение, не знаю как сократить
Приложения:
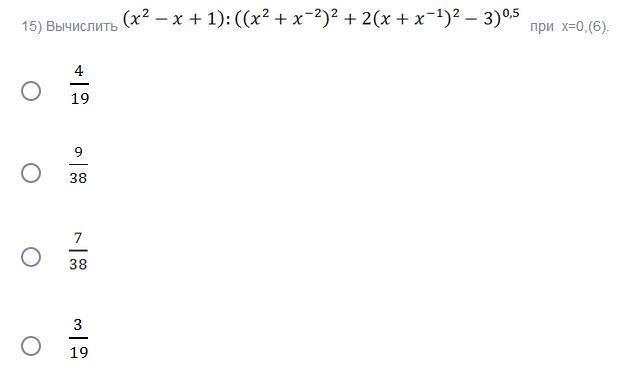
Ответы
Автор ответа:
1
Так как
,
тогда
.
и
При
Похожие вопросы
Предмет: Русский язык,
автор: ximk
Предмет: Русский язык,
автор: elephone
Предмет: Русский язык,
автор: семенка03
Предмет: Химия,
автор: drivexp
Предмет: Алгебра,
автор: juliapisockaya