Предмет: Алгебра,
автор: aanastasiaems
Помогите пожалуйста решить уравнение
Приложения:
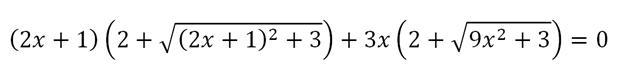
Аноним:
А где уравнение?
было минут 5 назад, зачем удалили? решили уже?
Ответы
Автор ответа:
1
Ответ:
-0.2
Объяснение:
Заметим, что левая и правая часть уравнения имеет общую структуру в виде функции:
Действительно, ведь
Исследует функцию f(t) на монотонность с помощью производной:
Так как , при любых t; t²≥0 при любых t, тогда
, при любых действительных t
Если f'(t)>0, то функция f(t) - возрастающая на всей числовой оси.
А для монотонных функций справедливо:
В нашем случае:
Похожие вопросы
Предмет: Русский язык,
автор: cvetkovadiana
Предмет: Русский язык,
автор: karenkar1
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: егорка141
Предмет: Математика,
автор: sofiksoko28032006