Предмет: Математика,
автор: kamil6860
найдите множество значений функции y= 1/sin^2x + 1/cos^2x
Приложения:
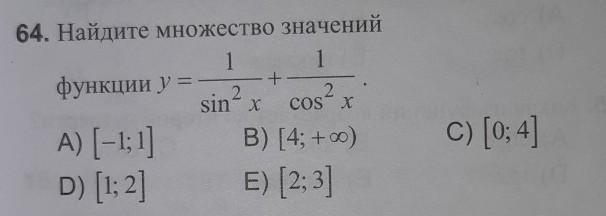
Ответы
Автор ответа:
1
Ответ:
в) [4; +∞)
Пошаговое объяснение:
Каждое из слагаемых положительное. При sin x=0 или cos x=0 получаем +∞, это верхняя грань. Если , то это нижняя грань.
.
Нижняя грань достигается и при значениях .
Значит область значений E(y)=[4;+∞).
Похожие вопросы
Предмет: Русский язык,
автор: olgasverkunova
Предмет: Русский язык,
автор: tacuky
Предмет: Русский язык,
автор: lilyacrimea
Предмет: Математика,
автор: dmitymihd