Предмет: Математика,
автор: shahzod77
В окружность с центром O вписана трапеция KLMN, в которой KL||MN, KL=8, MN=2, ∠NKL=45o. Хорда MA окружности пересекает отрезок KL в точке B такой, что KB=3. Найти расстояние от точки O до прямой AK. (ответ (19sqrt26)/26
antonovm:
Простая задача , но такая муторная
Ответы
Автор ответа:
2
Решение : /////////////////////////////////////////////
Приложения:
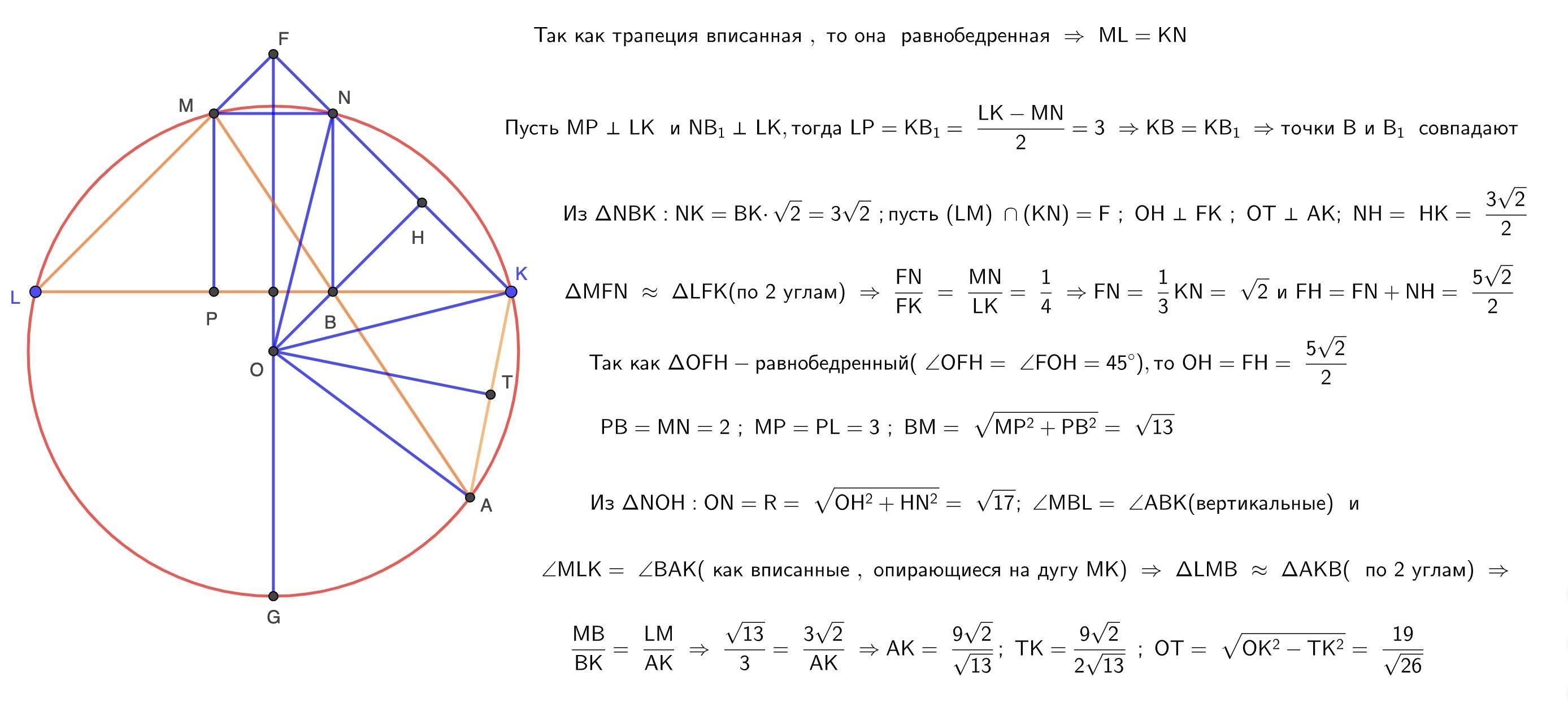
Центр описанной окружности - точка пересечения серединного перпендикуляра отрезка MN ( прямой , проходящей через середины оснований ) и серединного перпендикуляра отрезка NK
Автор ответа:
2
https://znanija.com/task/37834771
В окружность с центром O вписана трапеция KLMN, в которой KL || NM, LK=8 , NM=2, ∠NKL=45°. Хорда MA окружности пересекает отрезок KL в точке B такой, что KB=3. Найти расстояние от точки O до прямой AK.
Ответ: 19√26 / 26
Пошаговое объяснение: OH ⊥ KA ;
d = OH = √(OK² -KH²) = √( R² -(AK/2)²)
ΔLNK: LN/ sin(∠LNK) = 2R решение во вложении
Приложения:

Центр описанной около трапеции окружности ≡ центр описанной около треугольника LNK (←тупоугольный). * * * KML ; LMN или KNM * * *
Похожие вопросы
Предмет: Русский язык,
автор: Diana7777Love
Предмет: Русский язык,
автор: annapopova2
Предмет: Русский язык,
автор: Diana7777Love
Предмет: История,
автор: tanyavahomchik
Предмет: Математика,
автор: isya1991